Designs noise filters and simulates them to show how they attenuate white noise.

------------------------------------------------------------------------
See also CButter, StatePrp, Plot2D, WriteCM
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%  	Copyright 1994 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 1.
%--------------------------------------------------------------------------

Simulation parameters

%----------------------------
nSim      = 1000;

Filter parameters

%----------------------------
tSamp     = 0.5;
wCutoff   = 0.5;
nOrder    = 2;

% We have our lowest flex frequency at 0.3 Hz or 1.885 rad/sec
% Our control system bandwidth is 0.15 rad/sec
% So we want our cutoff to be 1 rad/sec
% The half sample frequency is 12.57 rad/sec so this is achievable
% The magnitude should be flat in the pass band

Call like this to get a plot

%-----------------------------
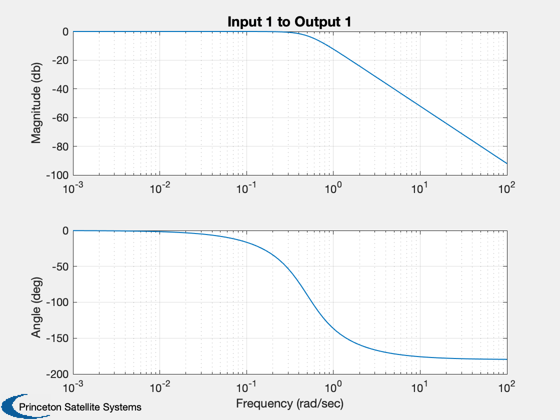
CButter(nOrder,wCutoff);

Get the discrete time equations

%--------------------------------
[a,b,c,d] = CButter(nOrder,wCutoff,tSamp,'Delta');

Write in C format

%------------------
fID = fopen('YawFilterMatrices','w');
WriteCM(fID,'A Matrix','fYawAMatrix',reshape(a',1,length(a)^2),12,20,nOrder)
WriteCM(fID,'B Matrix','fYawBMatrix',b,12,20,nOrder)
WriteCM(fID,'C Matrix','fYawCMatrix',c,12,20,nOrder)
WriteCM(fID,'D Matrix','fYawDMatrix',d,12,20,nOrder)
fclose(fID);

x     = zeros(length(a),1);
yPlot = zeros(1,nSim);
u     = randn(1,nSim);

for k = 1:nSim
  [yPlot(k),x] = StatePrp(a,b,c,d,x,u(k),'Delta');
end

fprintf('Filter Order       = %12i          \n',nOrder);
fprintf('Filter Cutoff      = %12.8f rad/sec\n',wCutoff);
fprintf('Sampling Period    = %12.8f sec    \n',tSamp);
fprintf('Mean               = %12.8f        \n',mean(yPlot));
fprintf('Attenuation        = %12.8f        \n', std(yPlot)/std(u));

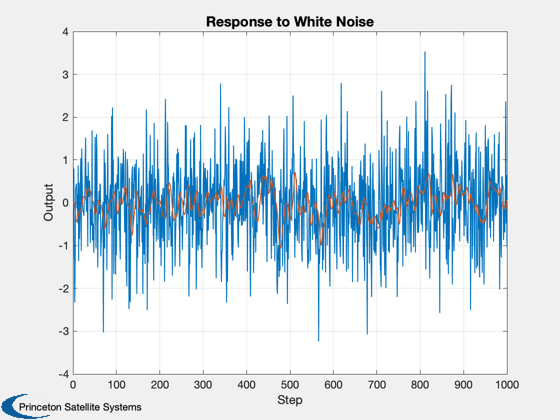
Plot2D(1:nSim,[u;yPlot],'Step','Output','Response to White Noise');


%--------------------------------------
% $Date$
% $Id: dae028a6d662be1a7d4351483ee1c0b765bb2adf $

Filter Order       =            2          
Filter Cutoff      =   0.50000000 rad/sec
Sampling Period    =   0.50000000 sec    
Mean               =  -0.02519277        
Attenuation        =   0.29844549        

Published with MATLAB® R2021b