Simulate a gravity turn trajectory in 2D.

The goal is to get the vehicle moving horizontally at orbital velocity.

Uses RHSLaunchVehicle2D which has a 'flat' earth. The simulation can handle any number of stages which are set by the arrays d.mSS, d.thrust, d.uE and d.cDA each of which have one element for each stage.

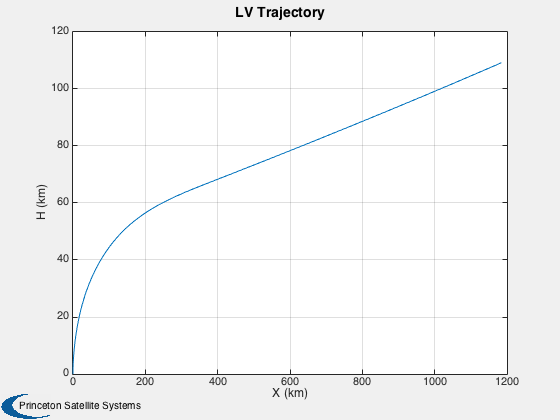
You vary the pitchover angle to get different trajectories. The number in the script gives the vehicle a horizontal trajectory (that begins to drop due to drag) at 53 km. The trajectory is very sensitive to gammaPitchover - on the order of a fraction of a degree.

------------------------------------------------------------------------
See also RHSLaunchVehicle2D, RK4, Plot2D, TimeLabl
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%    Copyright (c) 2007 Princeton Satellite Systems, Inc.
%    All Rights Reserved.
%-------------------------------------------------------------------------------

clear d;
dT   = 1;

Control

%--------
gammaPitchover = 10.5*pi/180; % rad
kPitch         = 30;          % steps

Vehicle model

%---------------
% For this demo vehicle, try pitchover of 10.5 degrees at 30 seconds
lv = struct;
lv.mSS          = [ 5000   600  400];  % Dry mass of each stage
lv.mSP          = [30000  8000  20];   % Fuel mass of each stage
lv.thrust       = [600 300 0.5];       % Thrust of each stage (kN)
lv.uE           = [285 285 252]*9.806*1e-3; % Exhaust velocity of each stage (m/s)
lv.mPLD         = 100;
lv.mDot         = lv.thrust ./ lv.uE;
lv.tBurn        = lv.mSP./lv.mDot;
% RHS data
d = LaunchRHSData( 2, lv );
d.cDA          = 0.35*[2 1 1]; % Drag coefficient of each stage times area

Initialization

nSim = floor(sum(lv.tBurn)/dT);

%-----------------------------------------
% [x  h  v  gamma massFuel]
%                x     Downrange distance
%                h     Altitude
%                v     Velocity
%                gamma Flight path angle
%-----------------------------------------
x = [0; 0; 0; pi/2; lv.mSP'];

disp('Initial acceleration should be positive:')
xDot = RHSLaunchVehicle2D( x, 0, d );
disp(xDot(3))

% Store plot points in x
%-----------------------
x = [x zeros(length(x),nSim)];

Initial acceleration should be positive:
       0.00380107726524317

Simulation

%------------
for k = 1:nSim

  % Initiate pitchover
  %-------------------
  if( k == kPitch )
    x(4,k) = pi/2 - gammaPitchover;
    fprintf(1,'\tPitch-over altitude: %f\n',x(2,k));
    fprintf(1,'\tPitch-over velocity: %f\n',x(3,k));
  end

  % Propagate one step
  %-------------------
  x(:,k+1) = RK4( @RHSLaunchVehicle2D, x(:,k), dT, k*dT, d );

  if( x(2,k+1) <= 0 )
    disp('Negative altitude (hit the earth), terminating.')
    break;
  end

end
nSim = k;
x    = x(:,1:(nSim+1));

	Pitch-over altitude: 1.877182
	Pitch-over velocity: 0.139398

Plotting

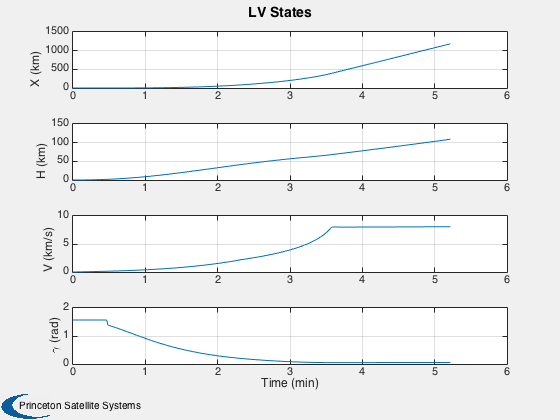
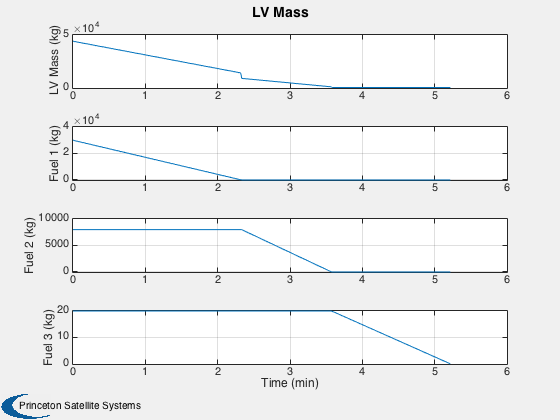
% Create the time array and label
%--------------------------------
[t, tL] = TimeLabl( (0:nSim)*dT );

% Plot the trajectory
%--------------------
Plot2D( x(1,:), x(2,:), 'X (km)', 'H (km)', 'LV Trajectory');

% Plot the states
%----------------
yL = {'X (km)' 'H (km)' 'V (km/s)' '\gamma (rad)'};
Plot2D( t, x(1:4,:), tL, yL, 'LV States');

% Compute the mass
%-----------------
m = zeros(1,nSim+1);
for k = 1:(nSim+1)
  mF   = x(5:end,k);
  j    = find(mF > 0,1,'first');
  m(k) = sum(mF) + sum(lv.mSS(j:end)) + lv.mPLD;
end

yL = {'LV Mass (kg)'};
for k = 1:length(mF)
  yL = {yL{:} sprintf('Fuel %i (kg)',k)};
end

% Plot the mass
%--------------
Plot2D( t, [m;x(5:end,:)], tL, yL, 'LV Mass');


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b