Compute the optimal flight path angle as a function of altitude.

The goal is a circular orbit. This script computes the optimal flight path angle at the time of separation after the second stage burn, to be on the desired transfer orbit to the final circular orbit. An angle of zero would indicate the perigee of a Hohmann transfer ellipse. The script allows for multiple burn segments with different exhaust velocities and thrust.

The engines in the example are a Merlin first stage, a J-2X second stage, and an AJ26-58 third stage.

The script also sizes an ellipsoid that can contain the volume of H2 and O2, based on the altitude with the minimum delta-V. This is needed by some drag models. ------------------------------------------------------------------------- See also RHSOptimalFPA, SurfaceAreaEllipsoidRevolution -------------------------------------------------------------------------

Constants
Mission data
Begin calculations
Plot
Calculate fuel volume and ellipsoids

%--------------------------------------------------------------------------
%   Copyright (c) 2013 Princeton Satellite Systems, Inc.
%   All rights reserved
%--------------------------------------------------------------------------

Constants

%-----------
mu        = Constant('mu earth');
rE        = 6378.14;
rhoH2     = 84;   % kg/m^3
rhoRP1    = 800;  % kg/m^3
rhoO2     = 1141; % kg/m^3
g         = 9.806;

Mission data

Define three segments

%----------------------
engine    = {'Merlin' 'J-2X' 'AJ26-58'};
mixRatio  = [ 2.24 5.5  2.24];
uE        = g*[ 311  448  331];
rhoFuel   = [rhoRP1 rhoH2 rhoRP1];

bC        = 2000/.05/4; % Ballistic coefficient
f        	= 4.5; % Ellipse coefficient
mDry      = 12000;

% Target conditions, Mach and altitude
% This example is from DARPA's XS-1
%-------------------
mach = 10;
hF   = 100*Constant('nmi to m')/1000;

% Compute as a function of 100 altitude points.
% This is the altitude achieved by the first stage.
%--------------------------------------------------
h = linspace(15,80);

Begin calculations

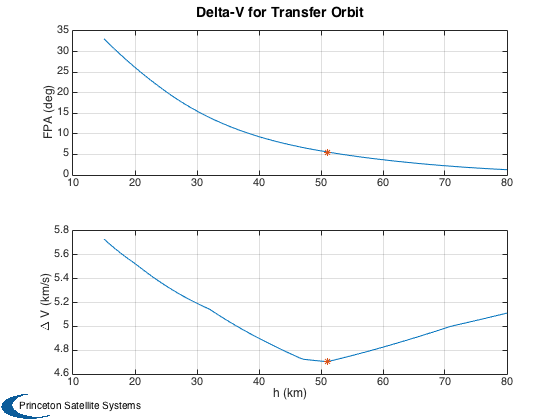
% Conditions at separation altitude
%----------------------------------
p = StdAtm(h*1000);
v = mach*p.speedOfSound/1000;

% Orbit radii
%------------
rF = rE + hF;
r0 = rE + h;

% Perform a numerical search for each specified altitude
%-------------------------------------------------------
n         = length(h);
dV        = zeros(1,n);
gamma     = zeros(1,n);
fprintf(1,'Perfoming fminsearch for %d points...\n',n);
for k = 1:n
   gamma(k)	= fminsearch( @RHSOptimalFPA, 0, [], h(k), hF, v(k), bC );
   dV(k)	= RHSOptimalFPA( gamma(k), h(k), hF, v(k), bC );
end
% Altitude producing the minimum delta-V
[dVMinH,kM] = min(dV);

Perfoming fminsearch for 100 points...

wE =

      7.29211542941961e-05

Plot

Plot2D(h,[gamma*180/pi;dV],'h (km)',{'FPA (deg)','\Delta V (km/s)'},'Delta-V for Transfer Orbit',[],{},{},1,[],1)
subplot(2,1,1)
hold on
plot(h(kM),gamma(kM)*180/pi,'*');
subplot(2,1,2)
hold on
plot(h(kM),dV(kM),'*');

Calculate fuel volume and ellipsoids

dVFirst     = 1954.9; % delta-V from the first stage
dVTotal     = dVMinH*1000 + dVFirst;
mR          = exp(dVTotal./uE);
mFuel       = mDry*mR - mDry;
mO2         = mixRatio.*mFuel./(1 + mixRatio);
mH2         = mFuel./(1 + mixRatio);
vol         = mO2/rhoO2 + mH2./rhoFuel;

% Find the ellipsoids enclosing the propellant
%---------------------------------------------
a = sqrt(3*f*vol/(4*pi));
c = a/f;
s = zeros(1,3);
for k = 1:3
	s(k)	= SurfaceAreaEllipsoidRevolution(a(k),c(k));
end
disp('Elliosiod surface areas (m^2)')
disp(s)


%--------------------------------------
% PSS internal file version information
%--------------------------------------