Design a simple aircraft control system consisting of a pitch rate tracking system.

------------------------------------------------------------------------
See also QECI, VTToVB, AC, ACBuild, ACInit, ACEngEq,
@acstate/acstate.m, C2DZOH, CLoopS, Altitude, Plot2D
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2002 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2.0 (ACT)
%--------------------------------------------------------------------------

The first step is to get the linearized plant model

%----------------------------------------------------

F16 database

%-------------
d               = ACBuild('F16');
d.theta0        = 0;
d.wPlanet       = [0;0;0];
d.actuator.name = 'F16Actuator';
d.aero.name     = 'ACAero';
d.engine.name   = 'ACEngine';
d.rotor.name    = [];
d.sensor.name   = 'ACSensor';
d.disturb.name  = [];

Load the standard atmosphere

%-----------------------------
d.atmData       = load('AtmData.txt');
d.atmUnits      = 'eng';

Actuator dynamics

%------------------
d.actuator.throttleLag = 4.9505e-02;
d.actuator.elevatorLag = 4.9505e-02;
d.actuator.aileronLag  = 4.9505e-02;
d.actuator.rudderLag   = 4.9505e-02;

Control settings

%-----------------
d.control.throttle  =   0.1385;
d.control.elevator  =  -0.7588;
d.control.aileron   =  -1.2e-7;
d.control.rudder    =   6.2e-7;

Initial state vector Corresponding to Nominal in Table 3.4-3 p. 139 of the reference

%-------------------------------------------------
altitude  = 100;
alpha     = 0.03691;
beta      = -4.0e-9;
theta     = 0.03991;
vT        = 502;
v         = VTToVB( vT, alpha, beta );

cG        = [0.35;0;0];

r         = [2.092565616797901e+07+altitude;0;0];

eulInit   = [0;theta;0.00];

q         = QECI( r, eulInit );
w         = [0;0;0];

wR        = 160;
engine    = ACEngEq( d, v, r ); % Engine state
mass      = 1/1.57e-3;
inertia   = [9497;55814;63100;0;-982;0];
actuator  = [0;0;0;0];
sensor    = [];
flex      = [];
disturb   = [];

Initial time and state

%-----------------------
x         = acstate( r, q, w, v, wR, mass, inertia, cG, engine, actuator, sensor, flex, disturb );

Generate the state space model

%-------------------------------
stateName.actuator = {'Throttle Lag', 'Elevator Lag', 'Aileron Lag', 'Rudder Lag'};
d                  = ACInit( x, d, stateName );
g                  = AC( x, 0, 0, d, 'linalpha');
aC                 = get( g, 'a' );
cC                 = get( g, 'c' );
bC                 = get( g, 'b' );

kLon         = [10 11 5 8 26];
kLonAQ       = [11 8 26];
kAlphaSensor = 5;
kQSensor     = 3;
kElevator    = 2;

disp('The state space matrices for just alpha and q')
a    = aC(kLonAQ,kLonAQ)
b    = bC(kLonAQ,kElevator);
c    = cC(kAlphaSensor,kLonAQ); % alpha only

disp('The plant eigenvalues')
eig(a)

The state space matrices for just alpha and q
a =
      -1.0167      0.90517   -0.0022528
      -1.2031      -1.2647     -0.18001
            0            0        -20.2
The plant eigenvalues
ans =
      -1.1407 +     1.0362i
      -1.1407 -     1.0362i
        -20.2 +          0i

First design the inner loop

%----------------------------
kAlpha   =  -0.08; % Notice this sign!
tauAlpha =   0.1;
aAlpha   =  -1/tauAlpha;
bAlpha   =   1/tauAlpha;
cAlpha   =   kAlpha;
dAlpha   =   0;

Test it in continuous mode

%---------------------------
aCL = CLoopS( a, b, c, aAlpha, bAlpha, cAlpha, dAlpha ); % This applies negative feedback

disp('Closed loop eigenvalues for the inner loop')
eig(aCL)

Closed loop eigenvalues for the inner loop
ans =
       -20.17 +          0i
       -10.16 +          0i
      -1.0758 +     1.3902i
      -1.0758 -     1.3902i

Now add the outer loop

%-----------------------
c    = cC([kAlphaSensor kQSensor],kLonAQ);
kI   =  1.5;
kQ   =  -0.5;
aCAS = [-1/tauAlpha 0;0 0];
bCAS = [1/tauAlpha 0;0 -1];
cCAS = [kAlpha kI];
dCAS = [0 kQ];

Test it in continuous mode

%---------------------------
aCL = CLoopS( a, b, c, aCAS, bCAS, cCAS, dCAS ); % This applies negative feedback

disp('Closed loop eigenvalues for the inner and outer loops')
eig(aCL)

dT           = 0.1; % 10 Hz controller works well

[a, b]       = C2DZOH( a, b,       dT );
[aCAS, bCAS] = C2DZOH( aCAS, bCAS, dT );

nSim         = 100;

xPlot        = zeros(1,nSim);

qC           = 1.0;
xCAS         = [0;0];
x            = [0;0;0];
y            = [0;0];

for k = 1:nSim

  xPlot(k) = y(2);

  y    = c*x;

  xCAS = aCAS*xCAS + bCAS*[y(1);y(2) - qC];
  yCAS = -(cCAS*xCAS + dCAS*y);

  x    = a*x + b*yCAS;

end

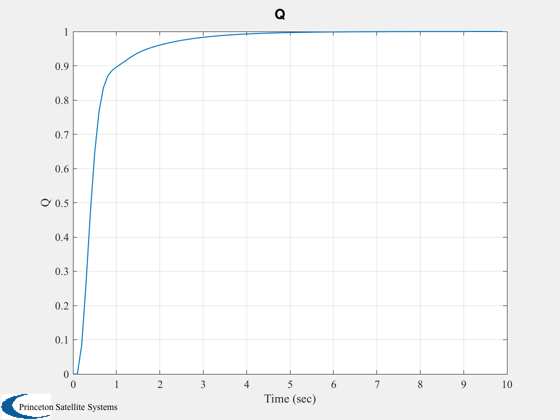
t = (0:(nSim-1))*dT;

Plot2D( t, xPlot, 'Time (sec)', 'Q' );

%--------------------------------------

Closed loop eigenvalues for the inner and outer loops
ans =
      -13.262 +          0i
      -10.879 +          0i
      -3.7436 +     3.3792i
      -3.7436 -     3.3792i
     -0.85305 +          0i

Published with MATLAB® R2019a