Simulate the linear and angular states of a rigid body using "AC.m"

Four different geometries are available to choose from.
A rotor may be included or omitted.

The motion is simulated using two different cases.
  case 0   --    The origin of the body frame coincides with the CG
  case 1   --    The origin of the body frame is translated to a non-CG
                 point

The inertias for case 0 and case 1 are different, according to the
parallel axis theorem.

The initial angular velocity is different for each case IF the inertia
matrix has non-zero off-diagonal terms.

No aerodynamic forces or torques are considered.

VERIFICATION
============

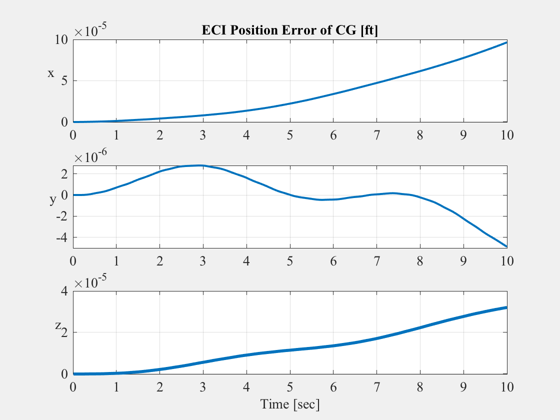
* The trajectories of both the CG and a non-CG point on the body are
  computed for each case, and the errors are plotted.

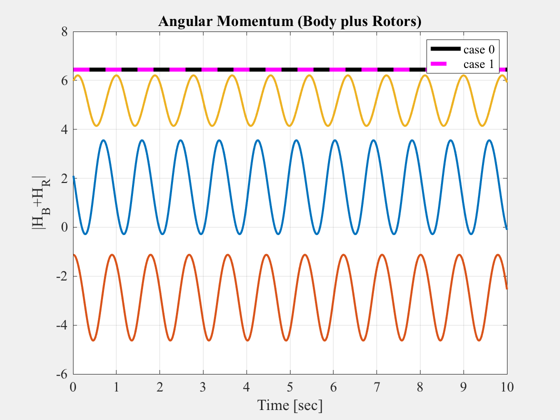
* The total angular momentum (body + rotors) is plotted.
  It should be constant.

------------------------------------------------------------------------
See also QECI, AC, ACInit, @acstate/acstate.m, IConv, QTForm,
TranslateAxes, Constant, TimeGUI, Cross, Dot, Mag, SkewSymm, Unit
------------------------------------------------------------------------

Paramters
Global for the time GUI
Set up database
Load the standard atmosphere
Control
mass
geometry
inertia matrix
cg location for cases 0, 1
Initial time and state
Initialize the model
Initialize the time display
Compute the angular momentum of the body about the CG for both cases
Compute the angular momentum of the rotors for both cases
Compute the CG position in ECI coordinates
Compute a non-CG position in ECI coordinates
Create the plots

%--------------------------------------------------------------------------
%    Copyright 2003 Princeton Satellite Systems, Inc.
%    All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2.0 (ACT)
%--------------------------------------------------------------------------

Paramters

%-------------------------

% rotor     (1)  Flag 0,1 -- indicating whether to include a rotor or not
rotor = 1;

% geometry  (1)  Number 1,2,3,4 -- indicating the type of geometry to use
%                 1 - Hemisphere                (inertia is pure diagonal)
%                 2 - Cylinder                  (inertia is pure diagonal)
%                 3 - Rectangular Tetrahedron   (inertia has off-diagonal terms)
%                 4 - Half-Cone                 (inertia has off-diagonal terms)
geometry = 4;

Global for the time GUI

%------------------------
global simulationAction
simulationAction = ' ';

Set up database

%----------------
d.mu            = 1.407644155238e+16;
d.name          = 'RigidBody';
d.theta0        = 0;
d.wPlanet       = [0;0;0];
d.actuator.name = [];
d.aero.name     = [];
d.engine.name   = [];
d.sensor.name   = [];
d.disturb.name  = [];
d.wind.name     = [];
d.flex          = [];

if( rotor )
   d.rotor.inertia = 2;
   d.rotor.u       = Unit([1;-2;3]);
   d.rotor.name    = [];
else
   d.rotor = [];
end

Load the standard atmosphere

%-----------------------------
d.atmData       = load('AtmData.txt');
d.atmUnits      = 'eng';

Control

%--------
d.control.throttle  =  0;
d.control.elevator  =  0;
d.control.aileron   =  0;
d.control.rudder    =  0;

mass

%-----
mass = 1;   % [slug]

geometry

%---------
switch geometry

case 1   % hemisphere

   R    = 2;   % radius
   mass = 1;   % mass [slug]

   % cg location (translated axes)
   cg   = [0;0;-3*R/8];

   % inertia elements (about CG)
   Ixx = (83/320)*mass*R^2;
   Iyy = (83/320)*mass*R^2;
   Izz =  (2/5)  *mass*R^2;
   Ixy = 0;
   Ixz = 0;
   Iyz = 0;

case 2   % cylinder

   R    = 3;   % radius
   L    = 10;  % length
   mass = 1;   % mass [slug]

   % cg location (translated axes)
   cg   = [0;0;-L/2];

   % inertia elements (about CG)
   Ixx = (1/4)*mass*R^2 + (1/12)*mass*L^2;
   Iyy = (1/4)*mass*R^2 + (1/12)*mass*L^2;
   Izz = (1/2)*mass*R^2;
   Ixy = 0;
   Ixz = 0;
   Iyz = 0;

case 3   % rectangular tetrahedron

   a = 1;      % x dimension
   b = 2;      % y dimension
   c = 3;      % z dimension

   % cg location (translated axes)
   cg   = [a;b;c]/4;

   % inertia elements (about CG)
   Ixx =  (3/80)*mass*(b^2 + c^2);
   Iyy =  (3/80)*mass*(a^2 + c^2);
   Izz =  (3/80)*mass*(a^2 + b^2);
   Ixy = -(1/80)*mass*a*b;
   Ixz = -(1/80)*mass*a*c;
   Iyz = -(1/80)*mass*b*c;

case 4   % half-cone

   R    = 2;   % radius
   L    = 5;   % length
   mass = 1;   % mass [slug]

   % cg location (translated axes)
   cg   = [0;-R/pi;-L/4];

   % inertia elements (about CG)
   Ixx = (3/20-1/pi/pi)*mass*R^2 + 3/80*mass*L^2;
   Iyy = (3/20)        *mass*R^2 + 3/80*mass*L^2;
   Izz = (3/10-1/pi/pi)*mass*R^2;
   Ixy = 0;
   Ixz = 0;
   Iyz = -1/(20*pi)*mass*R*L;

end

inertia matrix

%---------------
inertia0  = [Ixx;  Iyy;  Izz;  Ixy; Ixz; Iyz];     % inertia matrix, case 0
inertia1  = TranslateAxes( inertia0, -cg, mass );  % inertia matrix, case 1

cg location for cases 0, 1

%---------------------------
cG0       = [0;0;0];          % cg location in body frame, case 0
cG1       = cg;               % cg location in body frame, case 1

Re        = Constant('equatorial radius earth') * 1e3 / Constant('ft to m');
rCG       = [Re+150;0;0];     % initial ECI coordinates of CG (same for both cases)
vCG       = [15; 15; 0];      % initial velocity of CG in body frame (same for both cases)

i0        = IConv(inertia0);
i1        = IConv(inertia1);
m1        = SkewSymm(cG1);

wCG       = [0;2;0];          % angular velocity of rigid body in body frame (same for both cases)
HCG       = i0*wCG;           % angular momentum about CG
w0        = i0\(HCG);         % angular velocity, case 0 (should equal wCG)
w1        = (i1+m1*m1)\(HCG); % angular velocity, case 1 (will equal wCG if inertia matrix is diagonal)

eulInit   = [0;0;0];               % initial orientation (aligned x-north, y-east, z-down)
q         = QECI( rCG, eulInit );  % initial ECI to body quaternion (same for both cases

r0i       = rCG - QTForm(q,cG0);   % ECI coordinates of body frame origin, case 0
r1i       = rCG - QTForm(q,cG1);   % ECI coordinates of body frame origin, case 1

v0i       = vCG + Cross(w0,-cG0);  % initial velocity of origin in body frame, case 0
v1i       = vCG + Cross(w1,-cG1);  % initial velocity of origin in body frame, case 1

wR        = ones(length(d.rotor),1)*5;
engine    = [];
actuator  = [];
sensor    = [];
flex      = [];
disturb   = [];

Initial time and state

%-----------------------
t  = 0;
x0 = acstate( r0i, q, w0, v0i, wR, mass, inertia0, cG0, engine, actuator, sensor, flex, disturb );
x1 = acstate( r1i, q, w1, v1i, wR, mass, inertia1, cG1, engine, actuator, sensor, flex, disturb );

Initialize the model

%---------------------
dT   = 0.01;
nSim = 10/dT;

d0   = ACInit( x0, d );
d1   = ACInit( x1, d );

nR  = d0.nRotors;

r0  = zeros(3,nSim);
v0  = zeros(3,nSim);
q0  = zeros(4,nSim);
w0  = zeros(3,nSim);
wR0 = zeros(nR,nSim);
r1  = zeros(3,nSim);
v1  = zeros(3,nSim);
q1  = zeros(4,nSim);
w1  = zeros(3,nSim);
wR1 = zeros(nR,nSim);

Initialize the time display

%----------------------------
tToGoMem.lastJD        = 0;
tToGoMem.lastStepsDone = 0;
tToGoMem.kAve          = 0;
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, tToGoMem, 0, dT,...
    'Testing Equations of Motion for AC.m' );

for k = 1:nSim

   % Display the status message
   %---------------------------
   [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

   % Store for Plotting
   %-------------------
   r0(:,k) = get(x0,'r');
   v0(:,k) = get(x0,'v');
   q0(:,k) = get(x0,'q');
   w0(:,k) = get(x0,'w');
   r1(:,k) = get(x1,'r');
   v1(:,k) = get(x1,'v');
   q1(:,k) = get(x1,'q');
   w1(:,k) = get(x1,'w');

   wR0(:,k) = get(x0,'wR');
   wR1(:,k) = get(x1,'wR');

   % The simulation
   %---------------
   x0    = AC( x0, t, dT, d0  );
   x1    = AC( x1, t, dT, d1 );
   t     = t + dT;

   % Time control
   %-------------
   switch simulationAction
   case 'pause'
      pause
      simulationAction = ' ';
   case 'stop'
      return;
   case 'plot'
      break;
   end

end

TimeGUI('close');
t   = (1:k)*dT;
r0  = r0(:,1:k);
v0  = v0(:,1:k);
q0  = q0(:,1:k);
w0  = w0(:,1:k);
wR0 = wR0(:,1:k);
r1  = r1(:,1:k);
v1  = v1(:,1:k);
q1  = q1(:,1:k);
w1  = w1(:,1:k);
wR1 = wR1(:,1:k);

Compute the angular momentum of the body about the CG for both cases

%---------------------------------------------------------------------
H0   = i0*w0 - mass*Cross(cG0,Cross(w0,cG0));
H1   = i1*w1 - mass*Cross(cG1,Cross(w1,cG1));

Compute the angular momentum of the rotors for both cases

%----------------------------------------------------------
HR0 = zeros(3,k);
HR1 = zeros(3,k);
for i=1:nR
   HR0 = HR0 + d0.rotor(i).inertia*d0.rotor(i).u*(wR0(i,:)+Dot(d0.rotor(i).u,w0));
   HR1 = HR1 + d1.rotor(i).inertia*d1.rotor(i).u*(wR1(i,:)+Dot(d1.rotor(i).u,w1));
end


fprintf('2-norm of angular momentum difference: %f\n',norm( (H0+HR0)-(H1+HR1) ) )

2-norm of angular momentum difference: 0.000000

Compute the CG position in ECI coordinates

%-------------------------------------------
rCG0 = r0 + QTForm( q0, cG0 );
rCG1 = r1 + QTForm( q1, cG1 );
rCG3 = rCG*(t./t) + vCG*t - 0.5*[32.1;0;0]*(t.*t);

Compute a non-CG position in ECI coordinates

%---------------------------------------------
x     = -cG1;
rNCG0 = r0 + QTForm( q0, cG0 + x );
rNCG1 = r1 + QTForm( q1, cG1 + x );

Create the plots

%-----------------
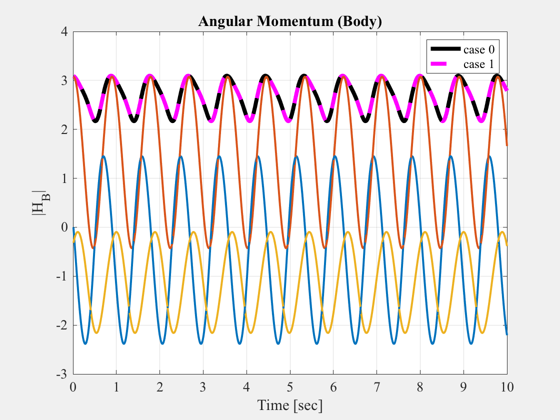
figure, plot(t,Mag(H0),'k',t,Mag(H1),'m--','linewidth',4), hold on
c = get(gca,'colororder');
c = [c(1:3,1:3); c(1:3,1:3)];
set(gca,'colororder',c)
plot(t,H0,t,H1,'--','linewidth',2), grid on, zoom on
title('Angular Momentum (Body)','fontsize',14)
legend('case 0','case 1');
ylabel('|H_B|','fontsize',14);
xlabel('Time [sec]','fontsize',14);
set(gca,'fontsize',14);

if( nR > 0 )
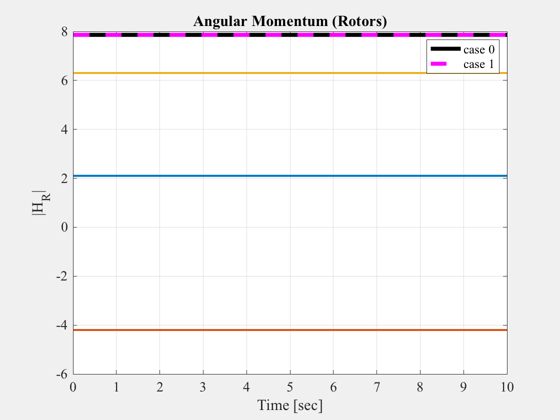
   figure, plot(t,Mag(HR0),'k',t,Mag(HR1),'m--','linewidth',4), hold on
   set(gca,'colororder',c)
   plot(t,HR0,t,HR1,'--','linewidth',2), grid on, zoom on
   title('Angular Momentum (Rotors)','fontsize',14)
   legend('case 0','case 1');
   ylabel('|H_R|','fontsize',14);
   xlabel('Time [sec]','fontsize',14);
   set(gca,'fontsize',14);
   figure, plot(t,Mag(H0+HR0),'k',t,Mag(H1+HR1),'m--','linewidth',4), hold on
   set(gca,'colororder',c)
   plot(t,H0+HR0,t,H1+HR1,'--','linewidth',2), grid on, zoom on
   title('Angular Momentum (Body plus Rotors)','fontsize',14)
   legend('case 0','case 1');
   ylabel('|H_B+H_R|','fontsize',14);
   xlabel('Time [sec]','fontsize',14);
   set(gca,'fontsize',14);
end

figure,
subplot(311)
plot(t,rCG0(1,:)-rCG1(1,:),'linewidth',2), grid on, zoom on,
set(gca,'fontsize',14)
title('ECI Position Error of CG [ft]','fontsize',14)
ylabel('x','rotation',0,'fontsize',14);
subplot(312)
plot(t,rCG0(2,:)-rCG1(2,:),'linewidth',2), grid on, zoom on,
set(gca,'fontsize',14)
ylabel('y','rotation',0,'fontsize',14);
subplot(313)
plot(t,rCG0(3,:)-rCG1(3,:),'linewidth',3), grid on, zoom on,
set(gca,'fontsize',14)
xlabel('Time [sec]','fontsize',14);
ylabel('z','rotation',0,'fontsize',14);

figure,
subplot(311)
plot(t,rNCG0(1,:)-rNCG1(1,:),'linewidth',2), grid on, zoom on,
set(gca,'fontsize',14)
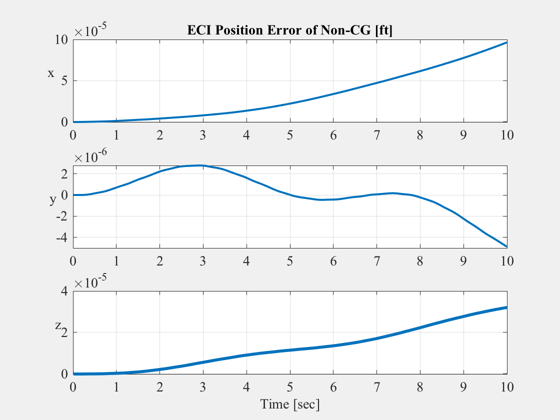
title('ECI Position Error of Non-CG [ft]','fontsize',14)
ylabel('x','rotation',0,'fontsize',14);
subplot(312)
plot(t,rNCG0(2,:)-rNCG1(2,:),'linewidth',2), grid on, zoom on,
set(gca,'fontsize',14)
ylabel('y','rotation',0,'fontsize',14);
subplot(313)
plot(t,rNCG0(3,:)-rNCG1(3,:),'linewidth',3), grid on, zoom on,
set(gca,'fontsize',14)
xlabel('Time [sec]','fontsize',14);
ylabel('z','rotation',0,'fontsize',14);

assignin('base','t', t );
assignin('base','q0',q0);
assignin('base','q1',q1);
assignin('base','r0',r0);
assignin('base','r1',r1);
assignin('base','v0',v0);
assignin('base','v1',v1);
assignin('base','w0',w0);
assignin('base','w1',w1);
assignin('base','i0',i0);
assignin('base','i1',i1);
assignin('base','cG0',cG0);
assignin('base','cG1',cG1);


%--------------------------------------

Simulate the linear and angular states of a rigid body using "AC.m"

Contents

Paramters

Global for the time GUI

Set up database

Load the standard atmosphere

Control

mass

geometry

inertia matrix

cg location for cases 0, 1

Initial time and state

Initialize the model

Initialize the time display

Compute the angular momentum of the body about the CG for both cases

Compute the angular momentum of the rotors for both cases

Compute the CG position in ECI coordinates

Compute a non-CG position in ECI coordinates

Create the plots