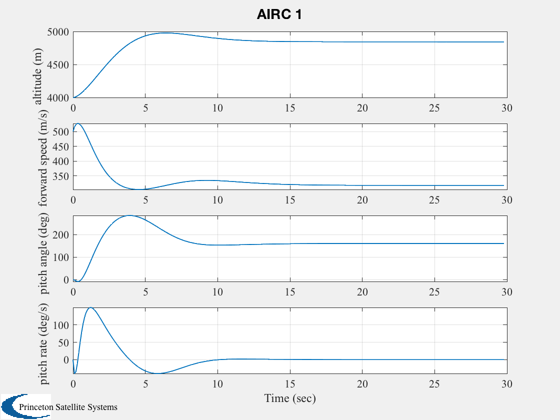
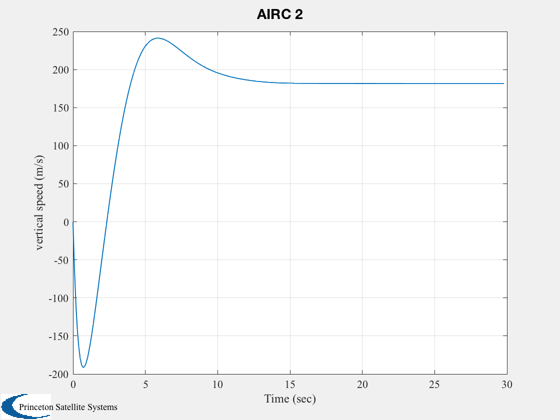
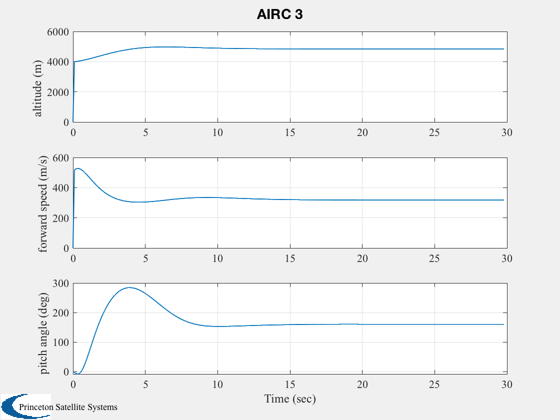
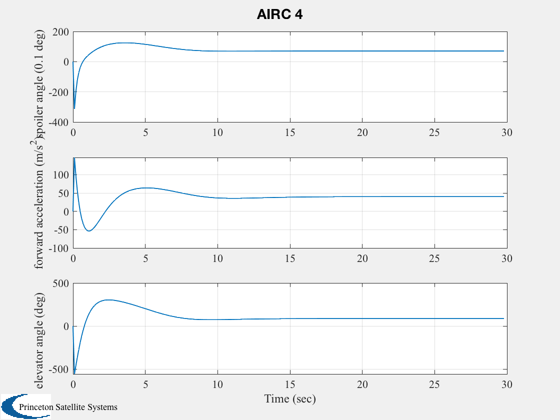
Longitudinal simulation using the AIRC aircraft model.

------------------------------------------------------------------------
See also StateSpacePlot, AIRC, CToD, LQC, PropStateSpace
------------------------------------------------------------------------

Contents

%---------------------------------------------------------------------------
%   Copyright 1999 Princeton Satellite Systems, Inc.
%   All rights reserved.
%---------------------------------------------------------------------------

Get the AIRC model

%-------------------
g = AIRC;

disp('The input vector')
get( g, 'inputs' )

disp('The output vector')
get( g, 'outputs' )

disp('The state vector')
get( g, 'states' )

The input vector
ans =
  3×28 char array
    'spoiler angle (0.1 deg)     '
    'forward acceleration (m/s^2)'
    'elevator angle (deg)        '
The output vector
ans =
  3×20 char array
    'altitude (m)        '
    'forward speed (m/s) '
    'pitch angle (deg)   '
The state vector
ans =
  5×20 char array
    'altitude (m)        '
    'forward speed (m/s) '
    'pitch angle (deg)   '
    'pitch rate (deg/s)  '
    'vertical speed (m/s)'

Time setup

%------------
tEnd = 30;
dT   = 0.1;
nSim = tEnd/dT;

Design a linear quadratic controller

%-------------------------------------
w    = [];
w.q  = eye( get(g,'n') );
w.r  = eye( get(g,'nI') );
w.qE = eye( get(g,'n') )/10;
w.rE = eye( get(g,'nO') );
gC   = LQC( g, w, 'lqg' );

Closed loop eigenvalues
ans =
            0 +          0i
      -0.4712 +     0.9458i
      -0.4712 -     0.9458i
    -0.017798 +    0.21302i
    -0.017798 -    0.21302i
      -4.4706 +          0i
      -1.1329 +     1.0025i
      -1.1329 -     1.0025i
      -1.5455 +   0.088722i
      -1.5455 -   0.088722i

Convert to discrete time

%-------------------------
g  = CToD( g,  dT, 'z' );
gC = CToD( gC, dT, 'z' );

Preallocate memory

%-------------------

Initialize the plotting

%------------------------
plots = struct('x','all','u','all','y','all','g',g);
d     = StateSpacePlot( 'init', plots, 400, nSim );

Initialize u and y

%-------------------
u    = zeros( get(g, 'nI'), 1 );
y    = zeros( get(g, 'nO'), 1 );

Initially at 4000 m altitude and 500 m/sec forward velocity

%------------------------------------------------------------
x  = [4000;500;0;0;0];

Initialize the controller

%-------------------------
xC = zeros(get(gC,'n'),1);
yC = x(1:3);

for k = 2:nSim

  % Plotting
  %---------
  d = StateSpacePlot( 'store', x, y, u, d );

  % Your controller here: u = f(y)
  %-------------------------------
  [xC, u] = PropStateSpace( gC, xC, y - yC );

  % The linear simulation
  %----------------------
  [x, y]  = PropStateSpace( g, x, u );

end

StateSpacePlot( 'plot', d )


%--------------------------------------

Published with MATLAB® R2019a