Demonstrate eigenvector assignment using a CCV Model
The example is taken from:
Stevens, B.L., Lewis, F.L. , Aircraft Control and Simulation, John Wiley & Sons, 1992, pp. 354-358.
------------------------------------------------------------------------ See also CCV, EVAssgnC, IC ------------------------------------------------------------------------
Contents
%-------------------------------------------------------------------------- % Copyright (c) 1997 Princeton Satellite Systems, Inc. % All rights reserved. %--------------------------------------------------------------------------
Plant matrix
%------------- disp(' ------------------------ Eigenvector Assignment ------------------------') g = CCV;
------------------------ Eigenvector Assignment ------------------------
Desired eigenvalues
%-------------------- j = sqrt(-1); lambda = [ -5.6 + j*4.2;... -5.6 - j*4.2;... -1.0;... -19.0;... -19.5]
lambda =
-5.6 + 4.2i
-5.6 - 4.2i
-1 + 0i
-19 + 0i
-19.5 + 0i
Desired eigenvectors
%--------------------- vD = [ 1-j 1+j 0 1 1;... -1+j -1-j 1 0 0;... 0 0 0 0 0];
We really want to decouple gamma
%--------------------------------- w = [ 1 1 1 1 1;... 1 1 1 1 1;... 100 100 1 1 1]; % The design matrix. One column per state % Each row relates vD to the plant matrix % For example, rows 7 and 8 relate column % 3 in vD to the plant. In this case % vD(1,3) relates to state 2 and vD(2,4) % relates to state 3. %---------------------------------------- d = [eye(3),zeros(3,2);... % Desired structure for eigenvector 1 eye(3),zeros(3,2);... % Desired structure for eigenvector 2 0 1 0 0 0;... % Desired structure for eigenvector 3 0 0 1 0 0;... % 0 0 0 1 0;... % Desired structure for eigenvector 4 0 0 0 0 1]; % Desired structure for eigenvector 5 % Rows in d per eigenvalue % Each column is for one eigenvalue % i.e. column one means that the first three rows of % d relate to eigenvalue 1 %--------------------------------------------------- rD = [3,3,2,1,1];
Compute the gain and the achieved eigenvectors
%----------------------------------------------- disp(' ') disp('----') disp('Gain') disp('----') [k, v] = EVAssgnC( g, lambda, vD, d, rD, w )
----
Gain
----
k =
-0.96896 -0.15349 -3.3999 -0.14628 0.76989
1.3765 0.26067 7.7643 0.46339 -1.2891
v =
Columns 1 through 2
0.22361 - 0.057239i 0.22361 + 0.057239i
-1.0079 + 1.1743i -1.0079 - 1.1743i
-0.0077639 + 0.0094276i -0.0077639 - 0.0094276i
0.7188 + 0.45808i 0.7188 - 0.45808i
-1.6308 - 0.37285i -1.6308 + 0.37285i
Columns 3 through 4
-1 + 0i -0.050762 + 0i
4.4832e-16 + 0i 1.0725 + 0i
1 + 0i -0.0056849 + 0i
-2.801 + 0i 1 + 0i
3.2331 + 0i 0 + 0i
Column 5
0.01058 + 0i
0.060078 + 0i
-0.013661 + 0i
0 + 0i
1 + 0i
Create the closed loop system
%------------------------------ [a, b, c ] = getabcd(g) aCL = a - b*k*c; disp(' ') disp('-----------------------') disp('Closed loop eigenvalues') disp('-----------------------') eig(aCL)
a =
-1.341 0.9933 0 -0.1689 -0.2518
43.223 -0.8693 0 -17.251 -1.5766
1.341 0.0067 0 0.1689 0.2518
0 0 0 -20 0
0 0 0 0 -20
b =
0 0
0 0
0 0
20 0
0 20
c =
0 1 0 0 0
47.76 -0.268 0 -4.56 4.45
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
-----------------------
Closed loop eigenvalues
-----------------------
ans =
-5.6 + 4.2i
-5.6 - 4.2i
-1 + 0i
-19 + 0i
-19.5 + 0i
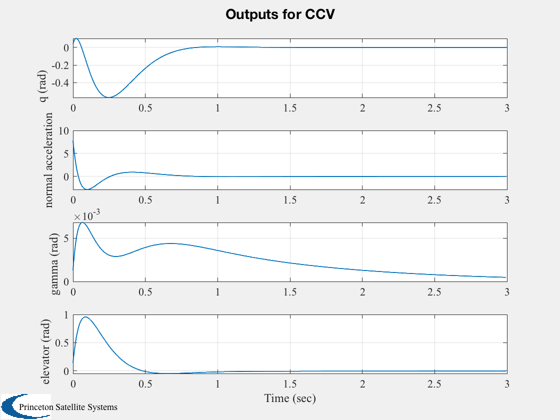
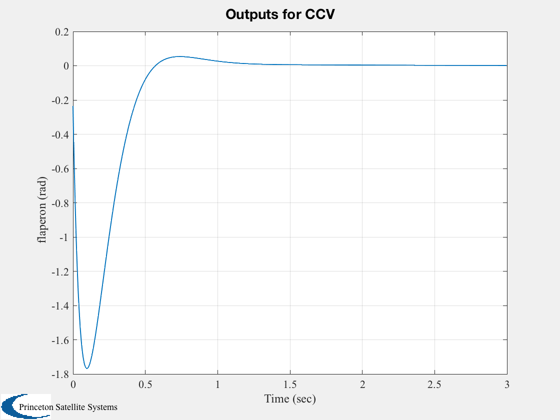
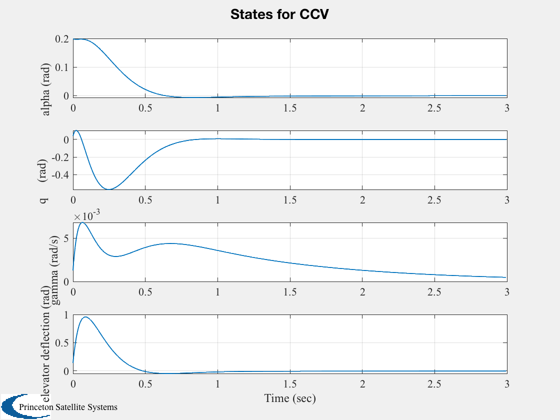
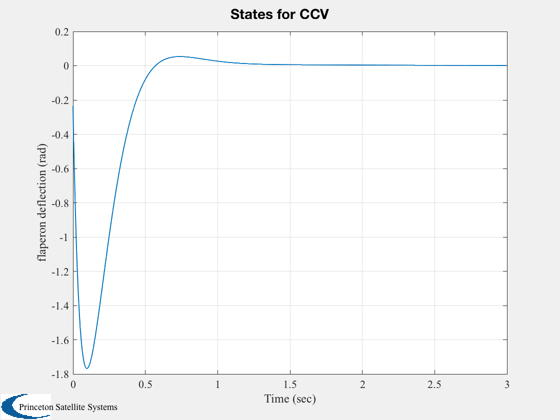
Simulate
%--------- g = set( g, aCL, 'a' ); x = [0.2;0;0;0;0]; IC( g, x, 0.005, 600 ); %--------------------------------------