Compare linear and non-linear simulations of an airship.

------------------------------------------------------------------------

-------------------------------------------------------------------------
See also EulNED, QECI, AC, ACInit, @acstate/acstate.m, AirshipLinMod,
AirshipStatespace, AirshipTrim, BuildAirshipModel, C2DZOH, Altitude,
QTForm, DeleteSuffix, Plot2D, Cross, Mag
-------------------------------------------------------------------------

Default parameters for demo
ensure proper formatting of "cmd" data structure
time step
time info
load airship model data
compute the linearized model
get state space matrices
discretize
reorganize matrices (optional)
dimensions
set up control vector
discrete state-space propagation
Non-Linear Sim
initial state
trim condition
compute the position and velocity of the CG
compute the angle of attack and sidelsip
compute the altitude
output
add initial values to yLin
Create the plots

%--------------------------------------------------------------------------
%    Copyright 2003 Princeton Satellite Systems, Inc.
%    All rights reserved.
%--------------------------------------------------------------------------

Default parameters for demo

%  Name of airship model
name  = 'ASM3';

% Location of origin (from nose)      [m]
xo    = 0;

% Initial altitude                    [m]
h     = 21336;

% Initial flight path angle           [rad]
theta = 0*pi/180;

% Initial angle of attack             [rad]
alpha = 0*pi/180;

% Initial linear velocity magnitude   [m/s]
V     = 15;

% Simulation time                     [sec]
tSim  = 100;

% command data structure
cmd.actuator = {'dELVL','dELVR'};   % which actuator  ('throttle','mu','dELVL','dELVR','dRUDB','dRUDT')
cmd.type     = {'step','step'};     % type of input   ('step','impulse')
cmd.value    = [1 1]*pi/180;        % value of applied control
cmd.tControl = 5;                   % start and stop times of applied control

ensure proper formatting of "cmd" data structure

%-------------------------------------------------
if( ~iscell(cmd.actuator) )
   cmd.actuator = {cmd.actuator};
end
if( ~iscell(cmd.type) )
   cmd.type = {cmd.type};
end

time step

%----------
dT   = 1;      % seconds;

time info

%----------
tSim = round(tSim/dT)*dT;
t    = 0:dT:tSim;
nSim = length(t);

load airship model data

%------------------------
disp('Building airship model...');
name = DeleteSuffix(name);
mdl  = BuildAirshipModel(name,xo);


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Linear Sim
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Building airship model...

compute the linearized model

%-----------------------------
useAlpha = 0;
g = AirshipLinMod( mdl, h, theta, alpha, V, useAlpha );

get state space matrices

%-------------------------
[a,b,c,d] = getabcd( g );

discretize

%-----------
[a, b]  = C2DZOH( a, b, dT );

reorganize matrices (optional)

%--------------------
% lat = 3+[1 3 4 6 8];             % phi, psi, p, r, v
% lon = 3+[2 5 7 9];               % theta, q, u, w
% a   = a([lon,lat],[lon,lat]);
% b   = b([lon,lat],:);
% c   = c(:,[lon,lat]);
%
% % forcibly change c here if desired
% c(10,:) = 0; c(10,4)=-1;

dimensions

%-----------
nX = length(a);
nU = size(b,2);
nY = size(c,1);

set up control vector

%----------------------
u      = zeros(nU,nSim);
nC     = length(cmd.actuator);
acts   = {'throttle','mu','dELVL','dELVR','dRUDB','dRUDT'};
kStart = cmd.tControl/dT+1;
for i=1:nC
   kAct = StringMatch(cmd.actuator{i},acts);
   if( strcmp( cmd.type{i}, 'impulse' ) )
      u(kAct,kStart) = cmd.value(i);
   elseif( strcmp( cmd.type{i}, 'step' ) )
      u(kAct,kStart:end) = cmd.value(i);
   end
end

discrete state-space propagation

%---------------------------------
disp('Running linear simulation...');
x    = zeros(nX,1);
yLin = zeros(nY,nSim);
xLin = zeros(nX,nSim);
for k = 1:nSim
   yLin(:,k) = c*x + d*u(:,k);
   x         = a*x + b*u(:,k);
   xLin(:,k) = x;
end

% now separate lat & lon
[gLat,gLon] = AirshipStatespace(g);
[a,b,c,d] = getabcd(gLat);
latStates = [1 2 4]; % p, r, beta
a = a(latStates,latStates);
b = b(latStates,:);
c = c(latStates,latStates);
d = d(latStates,:);
[a,b] = C2DZOH( a, b, dT );
x1    = zeros(3,1);
yLin1 = zeros(3,nSim);
xLin1 = zeros(3,nSim);
for k = 1:nSim
   rudk       = .5*(u(5,k)+u(6,k));
   ailk       = u(3,k)-u(4,k)+u(5,k)-u(6,k);
   yLin1(:,k) = c*x1 + d*[rudk;ailk];
   x1         = a*x1 + b*[rudk;ailk];
   xLin1(:,k) = x1;
end
[a,b,c,d] = getabcd(gLon);
[a,b] = C2DZOH( a, b, dT );
lonStates = [1 2 3];
a = a(lonStates,lonStates);
b = b(lonStates,:);
c = c(lonStates,lonStates);
d = d(lonStates,:);
x2    = zeros(3,1);
yLin2 = zeros(3,nSim);
xLin2 = zeros(3,nSim);
for k = 1:nSim
   elvk       = .5*(u(3,k)+u(4,k));
   yLin2(:,k) = c*x2 + d*[u(1:2,k);elvk];
   x2         = a*x2 + b*[u(1:2,k);elvk];
   xLin2(:,k) = x2;
end


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Running linear simulation...

Non-Linear Sim

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Re  = 6378.14*1e3;

initial state

%--------------
r0  = [Re+h;0;0];
v0  = V*[cos(alpha); 0; sin(alpha)];
q0  = QECI( r0, [0; theta+alpha; 0] );
w0  = zeros(3,1);
xNL = acstate( r0, q0, w0, v0, [], mdl.mass, mdl.inertia, mdl.cG, [], [], [], [], [] );
mdl = ACInit( xNL, mdl );

trim condition

%---------------
[T,trimMu,trimDELV]  = AirshipTrim( mdl, h, theta, alpha, V );
trimThrottle         = T/(2*mdl.engine.thrustMax);

r = zeros(3,nSim);
v = zeros(3,nSim);
q = zeros(4,nSim);
w = zeros(3,nSim);
e = zeros(3,nSim);

z = zeros(3,1);

disp('Running non-linear simulation...');
for k = 1:nSim

   % Store for Plotting
   %-------------------
   r(:,k) = get(xNL,'r');
   v(:,k) = get(xNL,'v');
   q(:,k) = get(xNL,'q');
   w(:,k) = get(xNL,'w');
   e(:,k) = EulNED( r(:,k), q(:,k), z );

   % controls
   %---------
   mdl.control.throttle = u(1,k) + trimThrottle;
   mdl.control.mu       = u(2,k) + trimMu;
   mdl.control.dELVL    = u(3,k) + trimDELV;
   mdl.control.dELVR    = u(4,k) + trimDELV;
   mdl.control.dRUDB    = u(5,k);
   mdl.control.dRUDT    = u(6,k);

   % The simulation
   %---------------
   xNL  = AC( xNL, t(k), dT, mdl  );

end

Running non-linear simulation...

compute the position and velocity of the CG

%--------------------------------------------
rCG = r + QTForm(q,mdl.cG);
vCG = v + Cross(w,mdl.cG);

compute the angle of attack and sidelsip

%-----------------------------------------
alpha = atan( -vCG(3,:)./vCG(1,:) );
beta  = asin( vCG(2,:)./Mag(vCG) );

compute the altitude

%---------------------
h = Altitude(rCG,'si');

output

%-------
y = [w; v; alpha; beta; e(1,:); h];

add initial values to yLin

%---------------------------
%yLin = yLin + y(:,ones(1,nSim));
y = y - y(:,ones(1,nSim));

Create the plots

%-----------------
tLab  = 'Time [sec]';
uLab  = {'throttle';'mu';'dELVL';'dELVR';'dRUDB';'dRUDT'};
p     = [y(1,:);  yLin(1,:); yLin1(1,:)]*180/pi;
q     = [y(2,:);  yLin(2,:); yLin2(1,:)]*180/pi;
r     = [y(3,:);  yLin(3,:); yLin1(2,:)]*180/pi;
vx    = [y(4,:);  yLin(4,:); yLin2(2,:)];
vy    = [y(5,:);  yLin(5,:); yLin1(3,:)];
vz    = [y(6,:);  yLin(6,:); yLin2(3,:)];
alpha = [y(7,:);  yLin(7,:);           ]*180/pi;
beta  = [y(8,:);  yLin(8,:);           ]*180/pi;
phi   = [y(9,:);  yLin(9,:);           ]*180/pi;
alt   = [y(10,:); yLin(10,:)           ];

u(2:6,:) = u(2:6,:)*180/pi;   % rad to deg

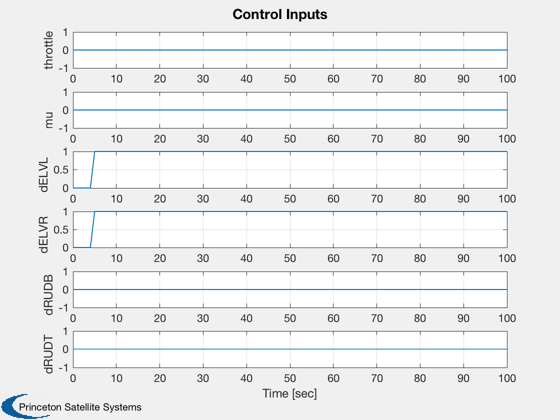
Plot2D( t, u(1:6,:), tLab, uLab,                 'Control Inputs'  )
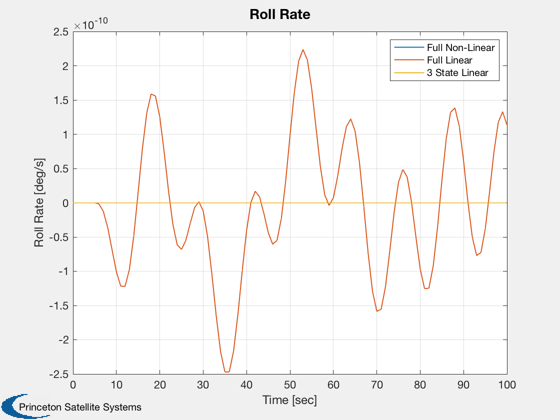
Plot2D( t, p,        tLab, 'Roll Rate [deg/s]',  'Roll Rate'       ), legend('Full Non-Linear','Full Linear','3 State Linear');
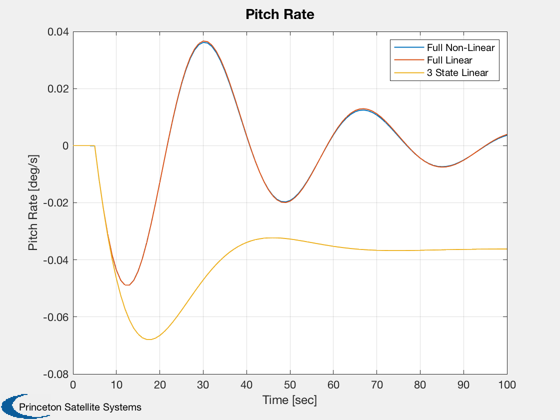
Plot2D( t, q,        tLab, 'Pitch Rate [deg/s]', 'Pitch Rate'      ), legend('Full Non-Linear','Full Linear','3 State Linear');
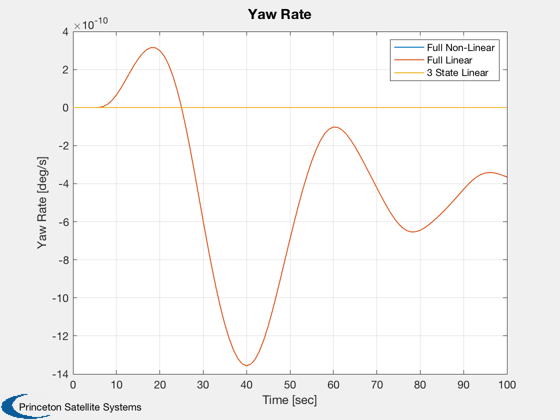
Plot2D( t, r,        tLab, 'Yaw Rate [deg/s]',   'Yaw Rate'        ), legend('Full Non-Linear','Full Linear','3 State Linear');
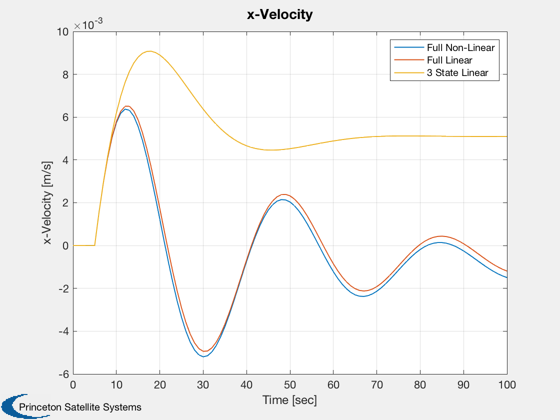
Plot2D( t, vx,       tLab, 'x-Velocity [m/s]',   'x-Velocity'      ), legend('Full Non-Linear','Full Linear','3 State Linear');
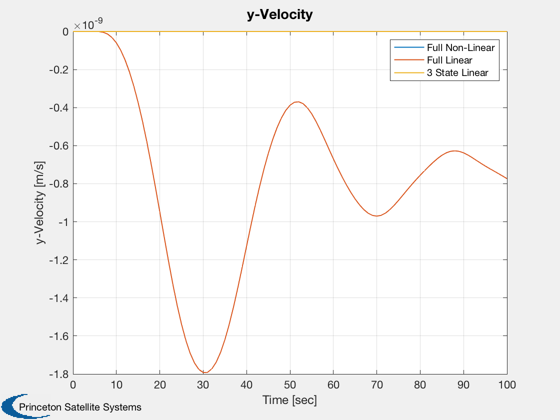
Plot2D( t, vy,       tLab, 'y-Velocity [m/s]',   'y-Velocity'      ), legend('Full Non-Linear','Full Linear','3 State Linear');
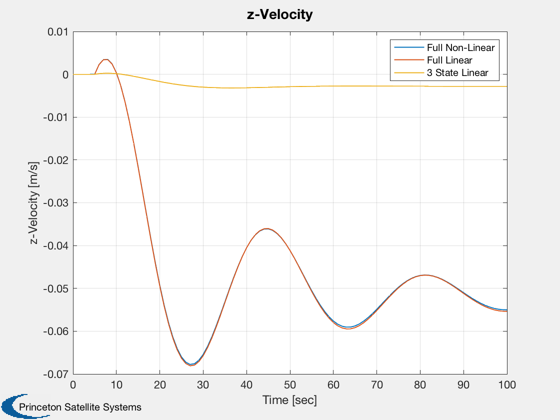
Plot2D( t, vz,       tLab, 'z-Velocity [m/s]',   'z-Velocity'      ), legend('Full Non-Linear','Full Linear','3 State Linear');
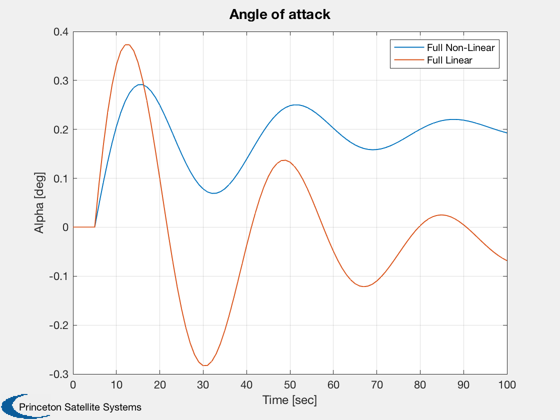
Plot2D( t, alpha,    tLab, 'Alpha [deg]',        'Angle of attack' ), legend('Full Non-Linear','Full Linear');
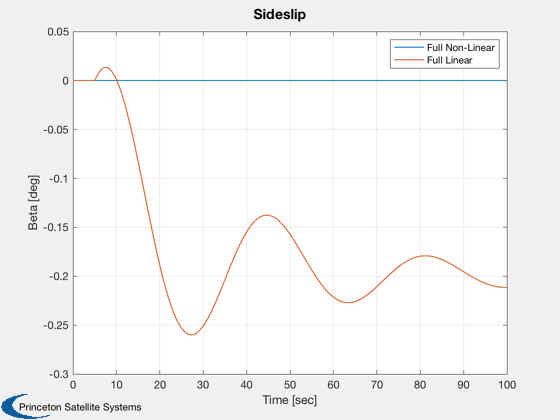
Plot2D( t, beta,     tLab, 'Beta [deg]',         'Sideslip'        ), legend('Full Non-Linear','Full Linear');
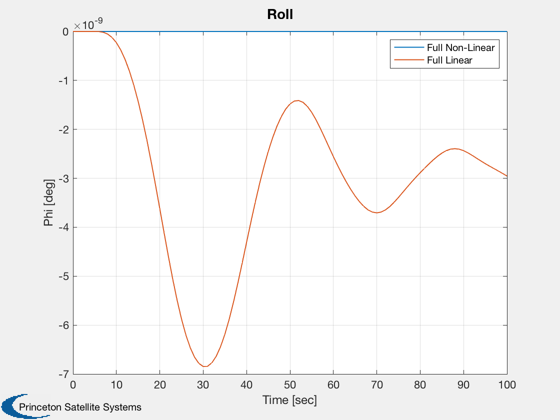
Plot2D( t, phi,      tLab, 'Phi [deg]',          'Roll'            ), legend('Full Non-Linear','Full Linear');
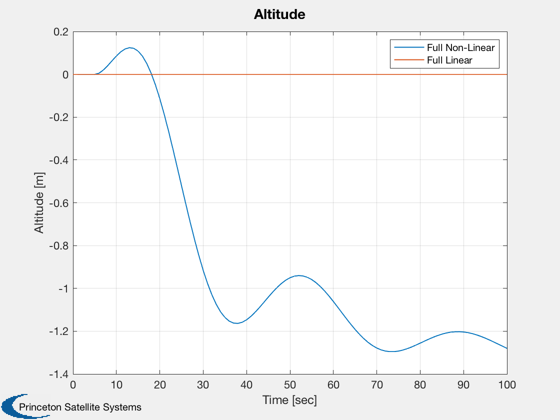
Plot2D( t, alt,      tLab, 'Altitude [m]',       'Altitude'        ), legend('Full Non-Linear','Full Linear');

fs  = 'fontsize';
rot = 'rotation';
lw  = 'linewidth';
ha  = 'horizontalalignment';
rt  = 'right';
NewFig('Airship Summary'),
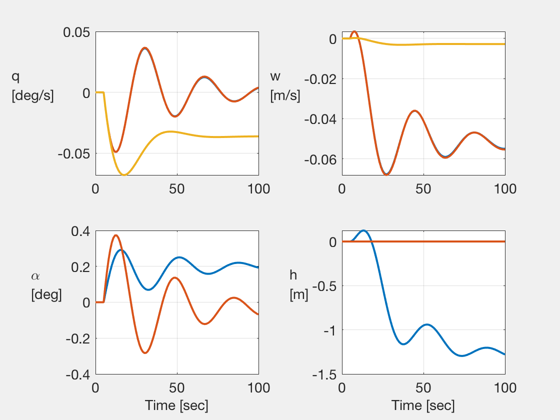
subplot(221), plot(t,q,lw,2),     grid on, set(gca,fs,14), ylabel('q\newline[deg/s]',   rot,0,fs,14,ha,rt);
subplot(222), plot(t,vz,lw,2),    grid on, set(gca,fs,14), ylabel('w\newline[m/s]',     rot,0,fs,14,ha,rt);
subplot(223), plot(t,alpha,lw,2), grid on, set(gca,fs,14), ylabel('\alpha\newline[deg]',rot,0,fs,14,ha,rt); xlabel('Time [sec]',fs,14);
subplot(224), plot(t,alt,lw,2),   grid on, set(gca,fs,14), ylabel('h\newline[m]',       rot,0,fs,14,ha,rt); xlabel('Time [sec]',fs,14);

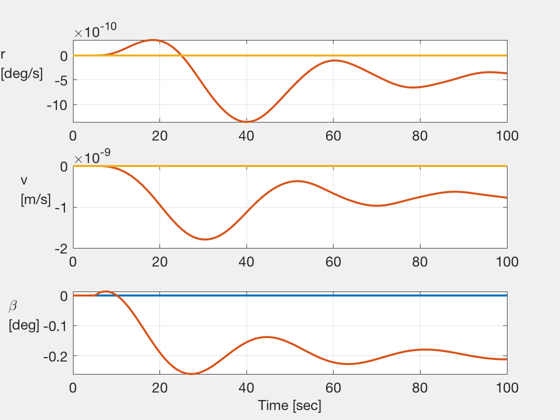
NewFig('Airship Summary'),
subplot(311), plot(t,r,lw,2),    grid on, set(gca,fs,14), ylabel('r\newline[deg/s]',   rot,0,fs,14,ha,rt);
subplot(312), plot(t,vy,lw,2),   grid on, set(gca,fs,14), ylabel('v\newline[m/s]',     rot,0,fs,14,ha,rt);
subplot(313), plot(t,beta,lw,2), grid on, set(gca,fs,14), ylabel('\beta\newline[deg]', rot,0,fs,14,ha,rt); xlabel('Time [sec]',fs,14);


%--------------------------------------

Compare linear and non-linear simulations of an airship.

Contents

Default parameters for demo

ensure proper formatting of "cmd" data structure

time step

time info

load airship model data

compute the linearized model

get state space matrices

discretize

reorganize matrices (optional)

dimensions

set up control vector

discrete state-space propagation

Non-Linear Sim

initial state

trim condition

compute the position and velocity of the CG

compute the angle of attack and sidelsip

compute the altitude

output

add initial values to yLin

Create the plots