Simulate the airship dynamic model.

------------------------------------------------------------------------

Runs a full nonlinear simulation of the specified airship model.
The simulation is open loop.

Computes a data structure with fields:
                    - t         Time
                    - r         ECI position of origin
                    - rCG       ECI position of CG
                    - v         velocity of origin in body frame
                    - vCG       velocity of CG in body frame
                    - q         ECI to body quaternion
                    - w         angular velocity of body frame
                    - alpha     angle of attack
                    - beta      sideslip
                    - force     aerodynamic force
                    - torque    aerodynamic torque

------------------------------------------------------------------------
See also AlphBeta, QECI, RNEH, AC, ACInit, AirData, @acstate/acstate.m,
AirshipTrim, BuildAirshipModel, AirshipAero, Altitude, IConv, QTForm,
Plot2D, TimeGUI, Cross, Mag, SkewSymm
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%    Copyright 2003 Princeton Satellite Systems, Inc.
%    All rights reserved.
%--------------------------------------------------------------------------

Demo parameters

% Initial angle of attack             [rad]
alpha = 5*pi/180;

% Initial sideslip angle              [rad]
beta  = 0;

% Initial linear velocity magnitude   [m/s]
V     = 15;

% Initial angular velocity vector     [rad/s]
w0    = [0;0;0];

% Initial altitude                    [m]
alt   = 21336;

% Elevator deflection, positive down  [rad]
elv   = [0;0];

% Rudder deflection, positive right   [rad]
rud   = [0;0];

% Location of origin (from nose)      [m]
xo    = 100;

% Simulation time                     [sec]
T     = 100;

% Trimming flag (1 trim, 0 do not)
trim = 1;

% flag to generate plots
doPlot = 1;

Global for the time GUI

%------------------------
global simulationAction
simulationAction = ' ';

Airship data

%-------------
d = BuildAirshipModel('ASM1',xo);

Trim

%-----
if( trim )
   [Thrust,mu,dElv]   = AirshipTrim( d, alt, 0, alpha, V );
   d.control.throttle = Thrust/(2*d.engine.thrustMax);
   d.control.mu       = mu;
   d.control.dELVL    = dElv;
   d.control.dELVR    = dElv;
else
   d.control.throttle = 0;
   d.control.mu       = 0;
   d.control.dELVL    = 0;
   d.control.dELVR    = 0;
end

Added Flap Deflections

%-----------------------
d.control.dELVL    = d.control.dELVL + elv(1);
d.control.dELVR    = d.control.dELVR + elv(2);
d.control.dRUDB    = rud(1);
d.control.dRUDT    = rud(2);

% initial position
Re        = 6378.14 * 1e3;       % equatorial radius of the earth
rCG       = [Re+alt;0;0];        % initial ECI coordinates of airship CG

% initial velocity
ta        = tan(alpha);
vx        = V*cos(beta)/sqrt(1+ta^2);
vy        = V*sin(beta);
vz        = vx*ta;
vCG       = [vx;vy;vz];
v0        = vCG - Cross(w0,d.cG);

% initial angular velocity
ss        = SkewSymm(d.cG);      % skew symmetric matrix
iCG       = IConv(d.inertiaCG);
iOrigin   = IConv(d.inertia);
HCG       = iCG*w0;                          % angular momentum about CG
w0        = (iOrigin+ss*ss*d.mass)\(HCG);    % angular velocity about origin (will not change if diagonal inertia)

% initial orientation
eulInit   = [0;0;pi/2];                % initial orientation (aligned x-north, y-east, z-down)
q         = QECI( rCG, eulInit );   % initial ECI to body quaternion

% adjust r0 to account for non-CG location of origin
r0        = rCG - d.cG;

wR        = ones(length(d.rotor),1)*5;
engine    = [];
actuator  = [];
sensor    = [];
flex      = [];
disturb   = [];

Initial time and state

%-----------------------
t = 0;
x = acstate( r0, q, w0, v0, wR, d.mass, d.inertia, d.cG, engine, actuator, sensor, flex, disturb );

Initialize the model

%---------------------
dT   = 0.25;
nSim = T/dT;

d  = ACInit( x, d );

r    = zeros(3,nSim);
v    = zeros(3,nSim);
q    = zeros(4,nSim);
w    = zeros(3,nSim);
f    = zeros(3,nSim);
trq  = zeros(3,nSim);

Initialize the time display

%----------------------------
tToGoMem.lastJD        = 0;
tToGoMem.lastStepsDone = 0;
tToGoMem.kAve          = 0;
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, tToGoMem, 0, dT, 'Airship Simulation' );

for k = 1:nSim

   % Display the status message
   %---------------------------
   [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

   % Store for Plotting
   %-------------------
   r(:,k)    = get(x,'r');
   v(:,k)    = get(x,'v');
   q(:,k)    = get(x,'q');
   w(:,k)    = get(x,'w');

   % Aero forces and moments
   %------------------------
   vAero         = v(:,k) + Cross(w(:,k),d.cG);
   altk          = Altitude(r(:,k),d.atmUnits);
   [alphk,betak] = AlphBeta(vAero);
   [mN,qBar,rho] = AirData( Mag( vAero ), altk, d.atmData, d.atmUnits );
   aero          = AirshipAero( alphk, betak, x, d.aero, qBar, d.control, d.flex, rho );
   f(:,k)        = aero.force;
   trq(:,k)      = aero.torque;

   % The simulation
   %---------------
   x = AC( x, t, dT, d  );
   t = t + dT;

   % Time control
   %-------------
   switch simulationAction
   case 'pause'
      pause
      simulationAction = ' ';
   case 'stop'
      doPlot = 0;
      return;
   case 'plot'
      break;
   end

end

TimeGUI('close');
t    = (1:k)*dT;
r    = r(:,1:k);
v    = v(:,1:k);
q    = q(:,1:k);
w    = w(:,1:k);
f    = f(:,1:k);
trq  = trq(:,1:k);

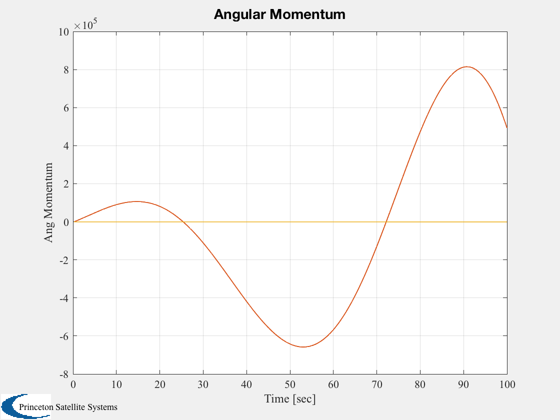
Compute the angular momentum of the body about the CG for both cases

%---------------------------------------------------------------------
H = IConv(d.inertia)*w - d.mass*Cross(d.cG,Cross(w,d.cG));

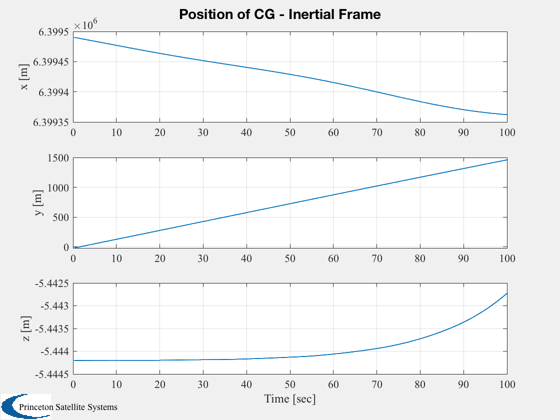
compute the position and velocity of the CG

%--------------------------------------------
rCG = r + QTForm(q,d.cG);
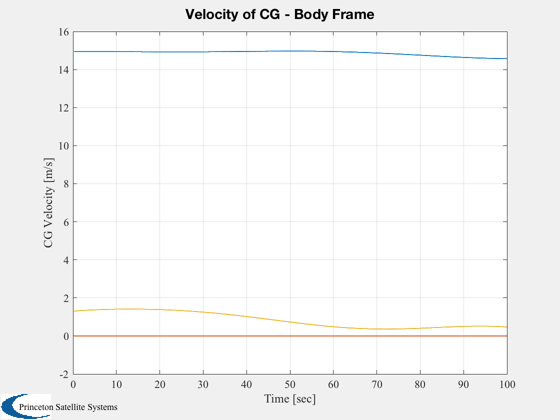
vCG = v + Cross(w,d.cG);

compute the angle of attack and sidelsip

%-----------------------------------------
alpha = atan( vCG(3,:)./vCG(1,:) )*180/pi;
beta  = asin( vCG(2,:)./Mag(vCG) )*180/pi;

save results in data structure

%-------------------------------
out.t      = t;
out.x      = x;
out.r      = r;
out.rCG    = rCG;
out.v      = v;
out.vCG    = vCG;
out.q      = q;
out.w      = w*180/pi;
out.alpha  = alpha;
out.beta   = beta;
out.force  = f;
out.torque = trq;

if( ~doPlot )
   return;
end

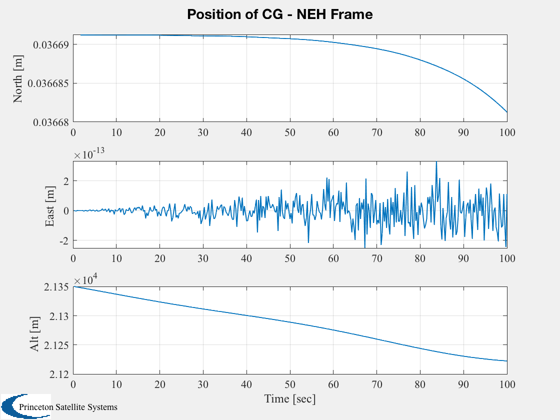
transform to the North-East-Up frame

%-------------------------------------
rneu = zeros(3,k);
for i=1:k
   rneu(:,i) = RNEH(rCG(:,i),'si');
end

Create the plots

%-----------------
Plot2D( t, H,     'Time [sec]', 'Ang Momentum',                      'Angular Momentum' ), grid on, zoom on
Plot2D( t, rCG,   'Time [sec]', {'x [m]';'y [m]';'z [m]'},           'Position of CG - Inertial Frame' )
Plot2D( t, rneu,  'Time [sec]', {'North [m]';'East [m]';'Alt [m]'},  'Position of CG - NEH Frame','lin' )
Plot2D( t, vCG,   'Time [sec]', 'CG Velocity [m/s]',                 'Velocity of CG - Body Frame' )
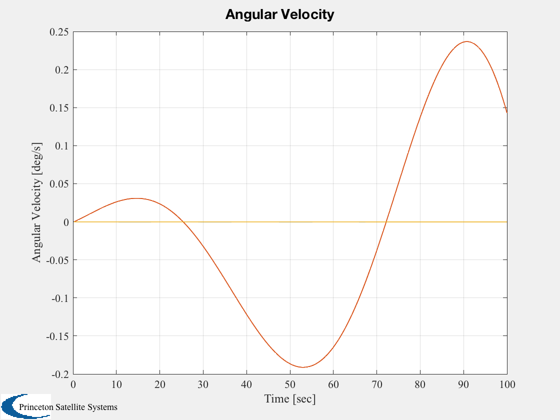
Plot2D( t, out.w, 'Time [sec]', 'Angular Velocity [deg/s]',          'Angular Velocity' )
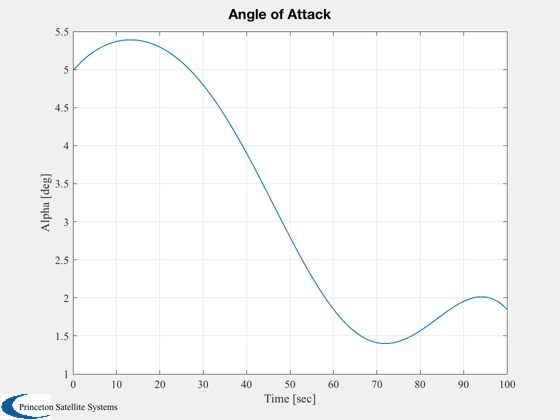
Plot2D( t, alpha, 'Time [sec]', 'Alpha [deg]',                       'Angle of Attack' )
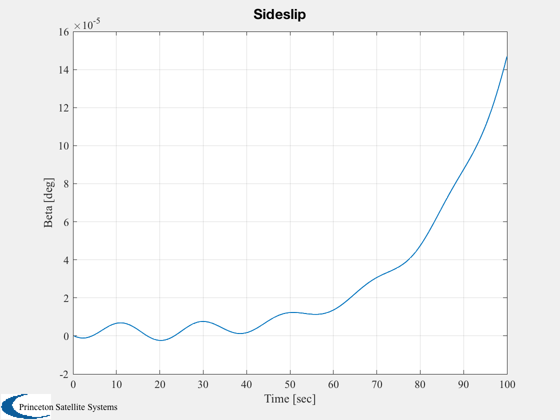
Plot2D( t, beta,  'Time [sec]', 'Beta [deg]',                        'Sideslip' )
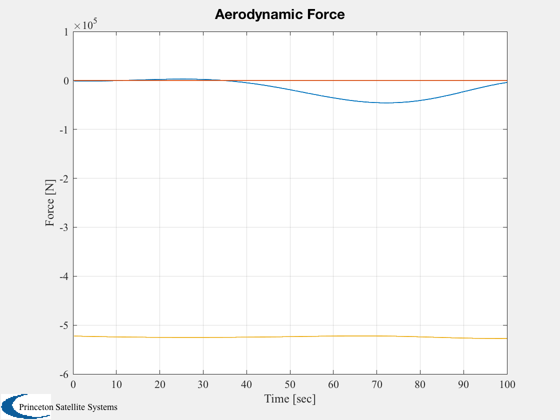
Plot2D( t, f,     'Time [sec]', 'Force [N]',                         'Aerodynamic Force' )
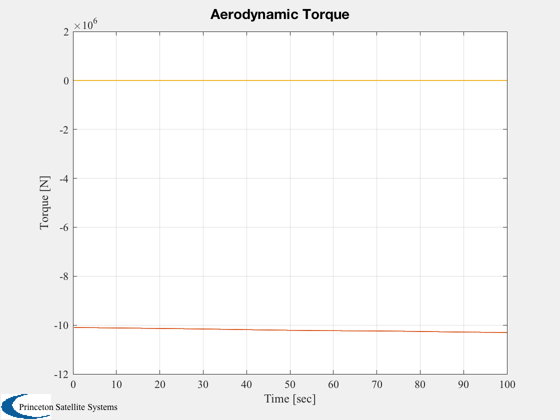
Plot2D( t, trq,   'Time [sec]', 'Torque [N]',                        'Aerodynamic Torque' )


%--------------------------------------

Published with MATLAB® R2019a