Demonstrates how to implement a digital filter.
Shows how to round off the coefficients for the filter.
Since version 1.
------------------------------------------------------------------------
See also S2Z, Plot2D
------------------------------------------------------------------------
Contents
Use a Tustin Transformation with a 0.1 sec sample period
[n,d] = S2Z(1,[1 1 1],0.1,'bilinear')
disp('The numerator coefficients are much smaller than the denominator')
disp('So extract 0.0024 from the numerator and write the filter in the form')
disp(' ')
disp('x(1) = -sum(d''*x) + sum(n''*u)')
disp('y = kX')
disp(' ')
disp('We want to round the coefficients to four decimal places')
disp('To get unity gain round -1.8955 up to -1.8954 because rounding it')
disp('does not move the poles.')
n =
0.0023753 0.0047506 0.0023753
d =
1 -1.8955 0.90499
The numerator coefficients are much smaller than the denominator
So extract 0.0024 from the numerator and write the filter in the form
x(1) = -sum(d'*x) + sum(n'*u)
y = kX
We want to round the coefficients to four decimal places
To get unity gain round -1.8955 up to -1.8954 because rounding it
does not move the poles.
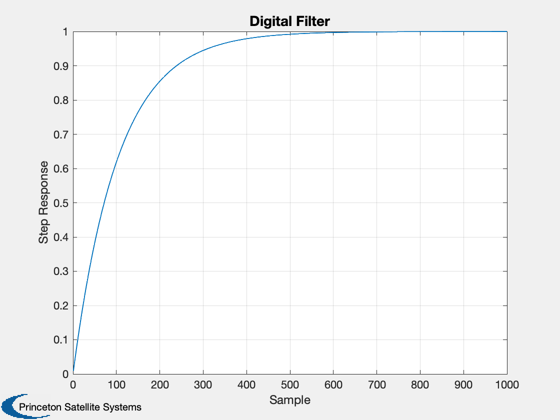
Unit step input
x = [0,0,0];
y = zeros(1,1000);
for k = 1:1000
x(3) = 1.8954*x(2) - 0.9050*x(1) + 1 + 2 + 1;
x(2) = x(3);
x(1) = x(2);
y(k) = 0.0024*x(3);
end
Plot the results
Plot2D(1:length(y),y,'Sample','Step Response','Digital Filter')