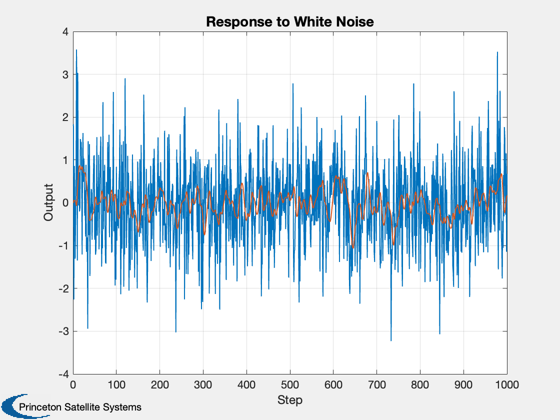
Designs noise filters and simulates them to show how they attenuate white noise.

Prints the output matrices to a text file in CommonData. ------------------------------------------------------------------------ See also CButter, StatePrp, Plot2D, WriteCM ------------------------------------------------------------------------

Simulation parameters
Filter parameters
Call like this to get a plot
Get the discrete time equations
Write in C format

%--------------------------------------------------------------------------
%  	Copyright 1994 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 1.
%--------------------------------------------------------------------------

Simulation parameters

%----------------------------
nSim      = 1000;

Filter parameters

%----------------------------
tSamp     = 0.5;
wCutoff   = 0.5;
nOrder    = 2;

% We have our lowest flex frequency at 0.3 Hz or 1.885 rad/sec
% Our control system bandwidth is 0.15 rad/sec
% So we want our cutoff to be 1 rad/sec
% The half sample frequency is 12.57 rad/sec so this is achievable
% The magnitude should be flat in the pass band

Call like this to get a plot

%-----------------------------
CButter(nOrder,wCutoff);

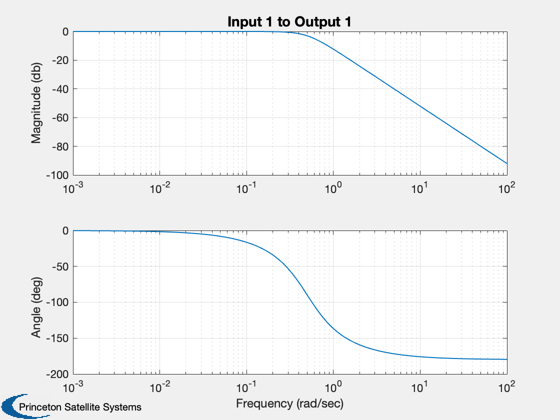
Get the discrete time equations

%--------------------------------
[a,b,c,d] = CButter(nOrder,wCutoff,tSamp,'Delta');

Write in C format

%------------------
p = FindDirectory( 'CommonData' );
fID = fopen(fullfile(p,'YawFilterMatrices.txt'),'w');
WriteCM(fID,'A Matrix','fYawAMatrix',reshape(a',1,length(a)^2),12,20,nOrder)
WriteCM(fID,'B Matrix','fYawBMatrix',b,12,20,nOrder)
WriteCM(fID,'C Matrix','fYawCMatrix',c,12,20,nOrder)
WriteCM(fID,'D Matrix','fYawDMatrix',d,12,20,nOrder)
fclose(fID);

x     = zeros(length(a),1);
yPlot = zeros(1,nSim);
u     = randn(1,nSim);

for k = 1:nSim
  [yPlot(k),x] = StatePrp(a,b,c,d,x,u(k),'Delta');
end

fprintf('Filter Order       = %12i          \n',nOrder);
fprintf('Filter Cutoff      = %12.8f rad/sec\n',wCutoff);
fprintf('Sampling Period    = %12.8f sec    \n',tSamp);
fprintf('Mean               = %12.8f        \n',mean(yPlot));
fprintf('Attenuation        = %12.8f        \n', std(yPlot)/std(u));

Plot2D(1:nSim,[u;yPlot],'Step','Output','Response to White Noise');


%--------------------------------------
% $Date$
% $Id: 6ca231ded9b2755736d54c2d5f7a70c8219445f5 $