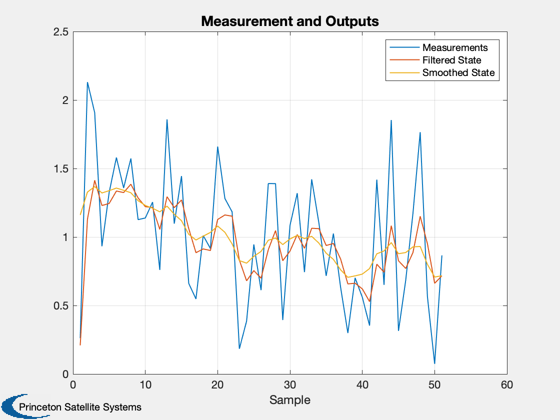
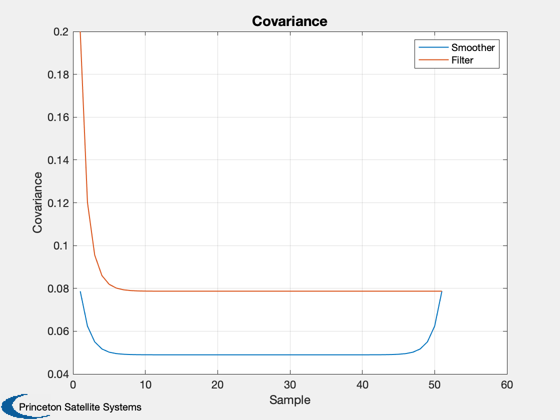
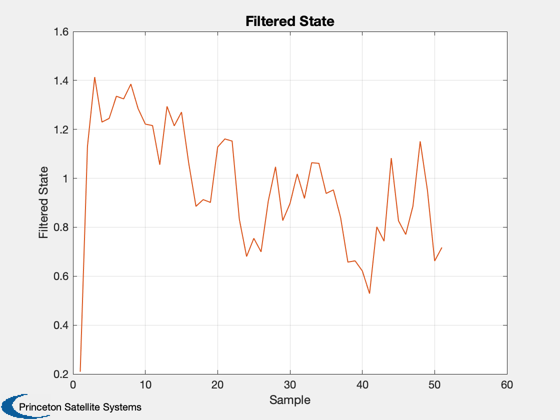
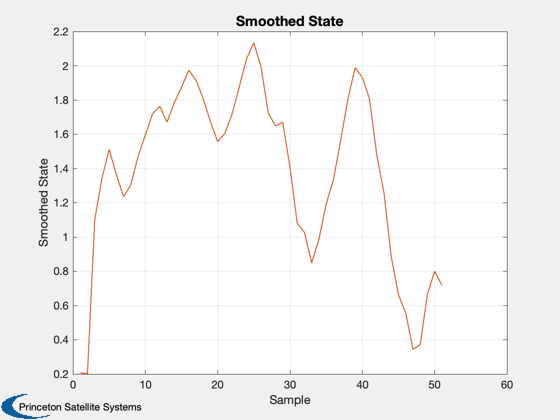
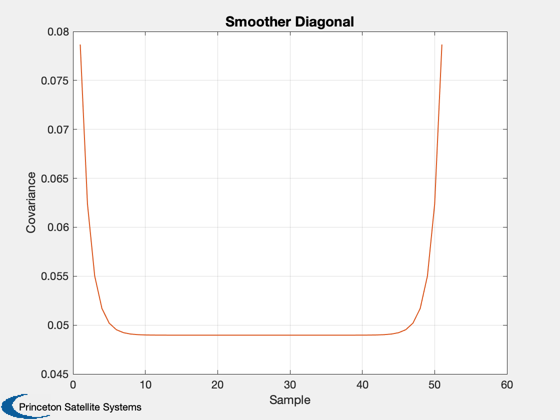
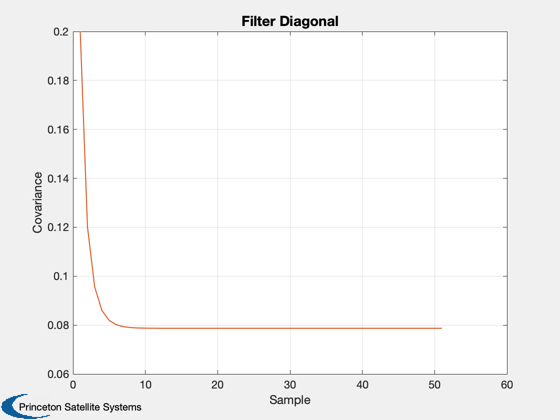
Demonstrate fixed interval smoothing using a Kalman Filter

Since version 1.
-------------------------------------------------------------------------
Reference: Brown, R.G., P.Y.C. Hwang, Introduction to Random Signals
           and Applied Kalman Filtering, Second Edition, p.238.
-------------------------------------------------------------------------
See also KSmooth
------------------------------------------------------------------------

Contents

Gauss Markov Process
The process
Make a higher order system

%-----------------------------------------------------------------------
%   Copyright 1996 Princeton Satellite Systems, Inc. All Rights Reserved.
%-----------------------------------------------------------------------

Gauss Markov Process

%---------------------
dT    = 0.02;
r     = 0.25;           % Measurement error covariance
h     = 1;              % Input matrix
phi   = exp(-dT);       % State transition matrix
q     = 1 - exp(-2*dT); % Plant noise covariance
nSamp = 51;

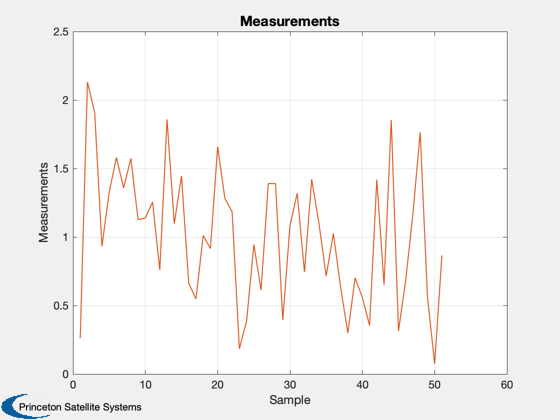
The process

%------------
u    = randn(1,nSamp);
y    = zeros(1,nSamp);
b    = sqrt(2)*(1 - phi);
y(1) = u(1);
for k = 2:nSamp
  y(k) = phi*y(k-1) + b*u(k);
end

z = y + 0.5*randn(1,nSamp);

Make a higher order system

%---------------------------

KSmooth( r, phi, q, h, z, 1 )

z   = [z;z];
phi = phi*eye(2);
q   =   q*eye(2);
h   =   h*eye(2);
r   =   r*eye(2);


KSmooth( r, phi, q, h, z, eye(2) )


%--------------------------------------
% PSS internal file version information
%--------------------------------------
% $Date$
% $Id: 7ce5076c04372fcbd7b02b175d07097f2ad2f78f $