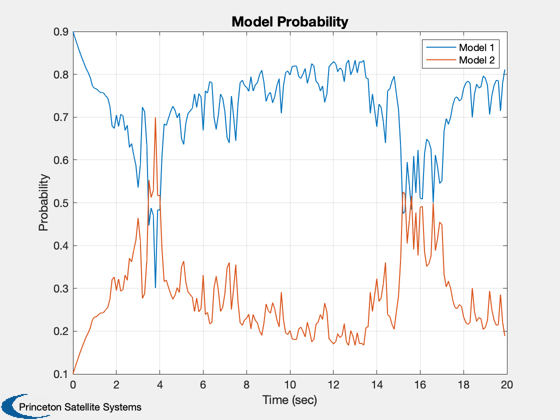
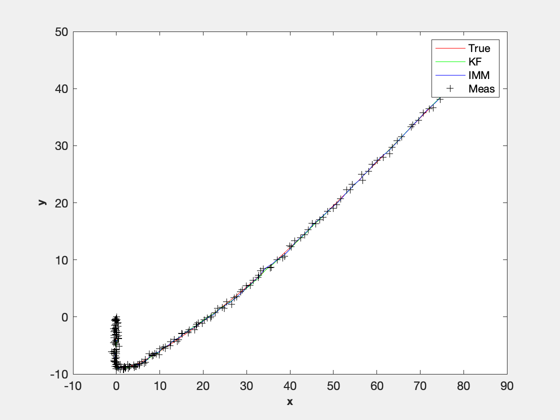
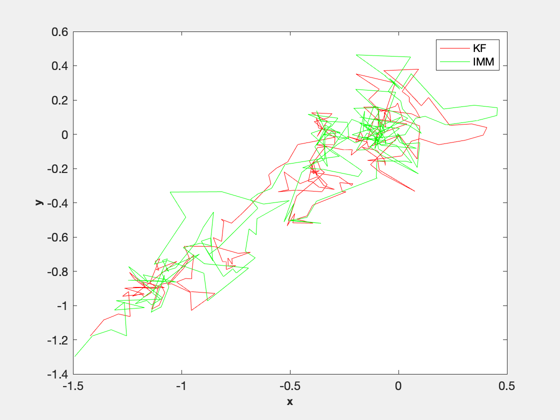
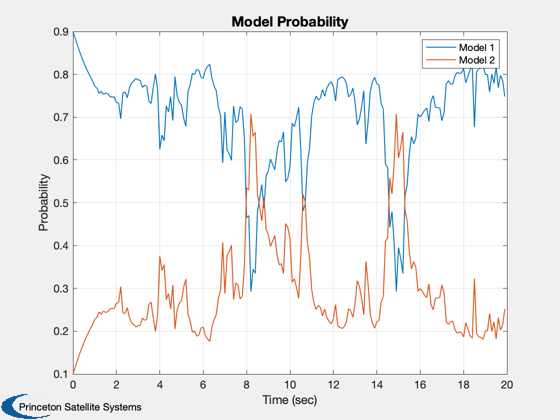
IMM test using a Continuous Wiener process acceleration (CWPA) model.

The model switches between two acceleration noise levels. It will print the two generated plots showing the trajectories and the trajectory errors.

Since version 11.

%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2012, 2014 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

% This loops for a Monte Carlo simulation
% Make zEnd > 1 for multiple simulations
%----------------------------------------
zEnd = 2;

meanKF = zeros(1,zEnd);
meanIMM = zeros(1,zEnd);

for z = 1:zEnd

  % Number of steps
  %----------------
  n           = 200;
  lowNoise    = 0.01;

  % The a priori covariance
  %------------------------
  p0	        = diag([0.1 0.1 0.1 0.1 0.5 0.5]);

  % Create the discrete time model
  %-------------------------------
  dT          = 0.1;
  [a, h, q]	= CWPAModel( dT );

  % When to use the different models
  %---------------------------------
  model          = ones(1,n);
  model( 51: 70) = 2;
  model(121:150) = 2;

  % Measurement noise
  %------------------
  r	= diag([0.1 0.1]);
  sR  = sqrt(r);

  % Process noise is only acceleration
  %-----------------------------------
  l2	= [0 0;0 0;0 0;0 0;1 0;0 1];
  l1	= l2*sqrt(lowNoise);

  % Run the simulation
  %-------------------
  x  = [0;0;0;-1;0;0];
  xS = zeros(6,n);
  y  = zeros(2,n);

  for k = 1:n
    xS(:,k) = x;
    y(:,k)  = h*x + sR*randn(2,1);
    if( model(k) == 1 )
        x = a*x + q*l1*randn(2,1);
    else
        x = a*x + q*l2*randn(2,1);
    end
  end

  % Test with the Kalman Filter
  %----------------------------
  mF	= zeros(6,n);
  m	= zeros(6,1);
  p	= p0;

  for k = 1:n
    mF(:,k) = m;
    [m, p]  = KFPredict( m, p, a, q*lowNoise );
    [m, p]  =  KFUpdate( m, p, y(:,k), h, r );
  end

  % Test with IMM
  %--------------
  mI	= zeros(6,n);
  m	= [0;0;0;-1;0;0];

  % The IMM data structure
  %------------------------
  dIMM.muI   = [0.9 0.1]; % Probability of being in mode 1 or 2
  dIMM.pIJ   = [0.98 0.02; 0.02 0.98]; % Transition probability
  dIMM.pI    = {p0 p0};
  dIMM.a     = {a a};
  dIMM.q     = {q*lowNoise q};
  dIMM.r     = {r r};
  dIMM.h     = {h h};
  dIMM.mI    = [m m];
  dIMM.use   = 'kf'; % Use a linear discrete Kalman Filter
  dIMM.m     = m;
  muI        = zeros(2,n);

  for k = 1:n
    mI(:,k) = dIMM.m;
    muI(:,k) = dIMM.muI;
    dIMM.y  = y(:,k);
    dIMM    = IMMPredict( dIMM );
    dIMM    =  IMMUpdate( dIMM );
  end

  % Plot the results
  %-----------------
  if( z == zEnd )
    NewFig('Trajectory')
    plot(xS(1,:),xS(2,:),'r',mF(1,:),mF(2,:),'g',mI(1,:),mI(2,:),'b',y(1,:),y(2,:),'k+');
    XLabelS('x')
    YLabelS('y')
    grid
    legend('True', 'KF', 'IMM', 'Meas')

    NewFig('Trajectory Error')
    plot(mF(1,:)-xS(1,:),mF(2,:)-xS(2,:),'r',mI(1,:)-xS(1,:),mI(2,:)-xS(2,:),'g');
    XLabelS('x')
    YLabelS('y')
    grid
    legend('KF', 'IMM')
  end

  meanKF(z)  = sum(sqrt((mF(1,:)-xS(1,:)).^2 + (mF(2,:)-xS(2,:)).^2))/n;
  meanIMM(z) = sum(sqrt((mI(1,:)-xS(1,:)).^2 + (mI(2,:)-xS(2,:)).^2))/n;

  [t, tL] = TimeLabl((0:(n-1))*dT);

  Plot2D( t, muI, tL, 'Probability', 'Model Probability')
  legend('Model 1', 'Model 2' );
end

mKF = mean(meanKF);
mIM = mean(meanIMM);

DispWithTitle( mKF, 'Mean KF');
DispWithTitle( mIM, 'Mean IMM');


%--------------------------------------
% PSS internal file version information
%--------------------------------------
% $Date$
% $Id: 6596e91f5e945e8b96fae12073e1accec9a00aeb $

grid =

     0     0     0     0     0     0
     0     0     0     0     0     0
     0     1     0     1     0     0
     0     1     0     1     1     0
     0     1     0     0     0     0
     0     0     0     0     0     0


grid =

     0     0     0     0     0     0
     0     0     0     0     0     0
     0     1     0     1     0     0
     0     1     0     1     1     0
     0     1     0     0     0     0
     0     0     0     0     0     0

Mean KF
      0.52087

Mean IMM
      0.47963

Published with MATLAB® R2021b