Contents

Discrete time Kalman filter for a nonlinear spring.

Loads the file KFSim.mat, generated by NLSpringSim.

------------------------------------------------------------------------
See also: C2DZOH, TimeLabl, Plot2D
------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2020 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2020.1
%--------------------------------------------------------------------------

Set up the filter

s           = load('KFSim');
n           = s.n; % Number of steps
r           = s.noiseMeas^2; % Measurement noise
q           = s.noiseForce^2; % Plant noise
h           = [1/s.w 0]; % Measurement matrix
a           = [0 1;-s.d.kL/s.d.m -s.d.c/s.d.m]; % State transition matrix
b           = [0; 1/s.d.m]; % Input matrix

% Discretize
[phi,gamma] = C2DZOH(a,b,s.dT);
xE          = [0;0]; % Estimated state
u           = s.d.f; % Input
p           = [0 0;0 0]; % Initial covariance
xP          = zeros(7,n);
e           = eye(2);

Run the Kalman Filter

for j = 1:n

  % Measurement
  z = s.xP(3,j);

  % Store variables to plot
  xP(:,j) = [z;diag(p);s.xP(1:2,j);xE];

  % Kalman Filter measurement update
  k  = p*h'/(h*p*h' + r);
  xE = xE + k*(z - h*xE);
  p  = (e - k*h)*p;

  % Kalman Filter state update
  xE = phi*xE + gamma*u;
  p  = phi*p*phi' + gamma'*q*gamma;

end

Plot

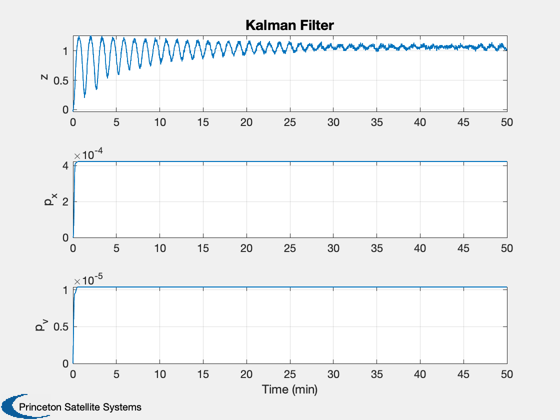
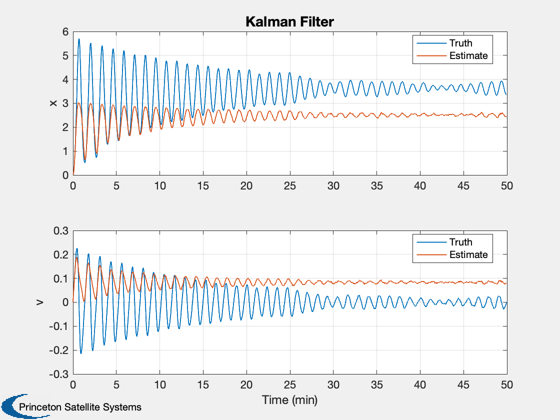
yL = {'z' 'p_x' 'p_v' 'x' 'v' };
lL = {{'Truth','Estimate'} {'Truth','Estimate'}};

[t,tL] = TimeLabl(0:(n-1)*s.dT);
Plot2D(t,xP(1:3,:),tL,yL(1:3),'Kalman Filter');
Plot2D(t,xP(4:7,:),tL,yL(4:5),'Kalman Filter',...
  'lin',{'[1 3]' '[2 4]'},[],[],[],[],lL);


%--------------------------------------
% $Date$
% $Id: c299f0c345ea40349d534f60b9d724dd9c1ba01d $

Published with MATLAB® R2021b