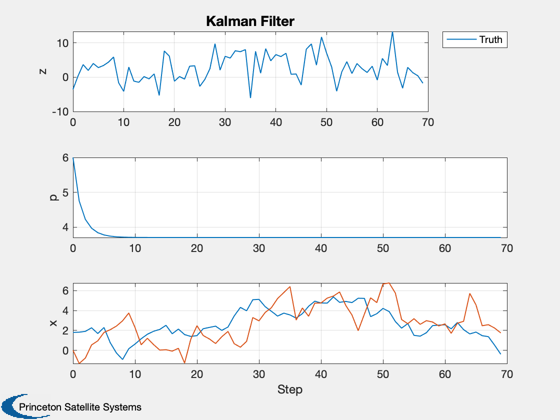
Discrete time Kalman filter

Model is a single integrator.

%--------------------------------------------------------------------------
%   Copyright (c) 2020 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2020.1
%--------------------------------------------------------------------------

n     = 70; % Number of steps
p0    = 6; % Initial covariance
r     = 10; % Measurement noise
q     = 1; % Plant noise
h     = 1; % Measurement matrix
phi   = 1; % State transition matrix
gamma = 1; % Input matrix
x     = 1; % Initial state
xE    = 0; % Estimated state
u     = 0; % Input
p     = p0;

xP    = zeros(4,n);
for j = 1:n

	% Truth model
  z = h*x + sqrt(r)*randn; % Measurement
  x = phi*x + gamma*u + sqrt(q)*randn;

  % Store variables to plot
  xP(:,j) = [z;p;x;xE];

  % Kalman Filter
  k  = p*h'/(h*p*h' + r);
  xE = xE + k*(z - h*xE);
  p  = (1 - k*h)*p; % Measurement update of covariance

  xE = phi*xE + gamma*u;
  p  = phi*p*phi' + gamma*q*gamma';

end

yL = {'z' 'p' 'x'};

Plot2D(0:n-1,xP,'Step',yL,'Kalman Filter','lin',{'1' '2' '[3 4]'});

legend('Truth','Estimate','location','bestoutside')

%--------------------------------------
% $Date$
% $Id: e70f63d3c6c632e441dd4328ade4adf184b821d0 $

Warning: Ignoring extra legend entries. 

Published with MATLAB® R2021b