Demonstrate the Kalman Filter using UD factorization.

Since version 9.
------------------------------------------------------------------------
See also UDKalmanFilter., C2DZOH, KFilter, Plot2D
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright 1999 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Double integrator plant

%------------------------
a = [0 1;0 0];
b = [0;1];

Measuring position

%-------------------
h = [1 0];

Time step

%----------
dT = 0.5;

Discretize

%-----------
[phi,gam] = C2DZOH(a,b,dT);

p       = 5*eye(2);
z1Sigma = 0.1;
r       = z1Sigma^2;
q       = eye(2);
xEst    = [1;2];

Create the UD form

%-------------------
d   = UDKalmanFilter( 'p to ud', p        );
d   = UDKalmanFilter( 'add q',   d, q     );
d   = UDKalmanFilter( 'add g',   d, eye(2));
d   = UDKalmanFilter( 'add phi', d, phi   );
d   = UDKalmanFilter( 'add r',   d, r     );
d   = UDKalmanFilter( 'add x',   d, xEst  );
d   = UDKalmanFilter( 'add h',   d, h     );

Initialize the simulation

%--------------------------
x     = [0;0];
nSim  = 10;
xPlot = zeros(10,nSim);

for j = 1:nSim

  % Plotting
  %---------
  xPlot(:,j)   = [x;xEst;d.x;diag(p);diag(UDKalmanFilter('compute p',d))];

  % Measurement with random noise
  %------------------------------
  z            = h*x + z1Sigma*randn;

  % Conventional Kalman Filter
  %---------------------------
  [xEst, p, k] = KFilter( r, phi, q, h, xEst, z, p );

  % UD Kalman Filter
  %-----------------
  d            = UDKalmanFilter( 'incorporate measurement', d, z );
  d            = UDKalmanFilter( 'propagate', d );

  % Plant
  %------
  x            = phi*x;
end

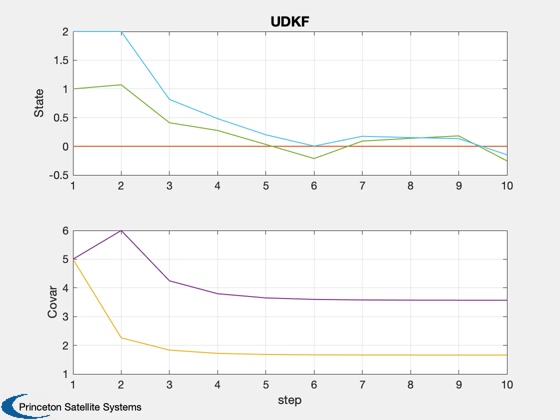
Plot2D( 1:nSim, xPlot, 'step',['State';'Covar'],'UDKF','lin',['1:6 ';'7:10'])
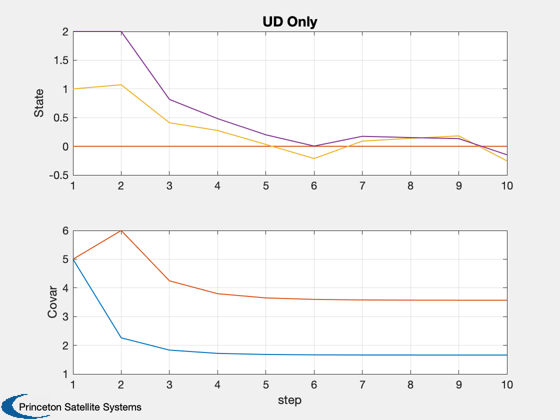
Plot2D( 1:nSim, xPlot([1 2 5 6 9 10],:), 'step',['State';'Covar'],'UD Only','lin',['1:4';'5:6'])
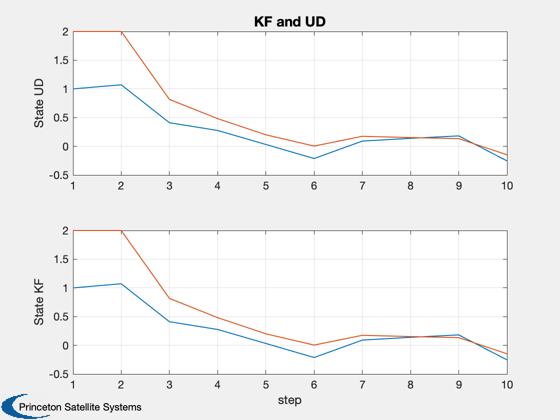
Plot2D( 1:nSim, xPlot([3 4 5 6],:), 'step',['State UD';'State KF'],'KF and UD','lin',['1:2';'3:4'])


%--------------------------------------
% PSS internal file version information
%--------------------------------------
% $Date$
% $Id: 045f617c1bfa2ae87a53f87352043b99dc57deb1 $

Published with MATLAB® R2021b