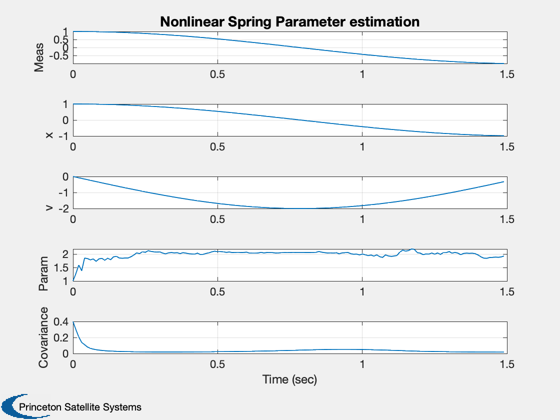
Demonstrate UKF parameter estimation with a nonlinear spring example.

------------------------------------------------------------------------
See also Plot2D, RK4, UKFP
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2017.1
%--------------------------------------------------------------------------

nSim          = 150;
dRHS.zeta     = 0; % Damping
dRHS.w        = 2; % Natural frequency
dRHS.m        = 1;
sigY          = 0.0001;
xP            = zeros(5,nSim);
x             = [1;0];
dT            = 0.01;

Estimation parameters

%----------------------
d.x           = x;
d.p           = 0.4;
d.int         = 'RK4';
d.rHSFun      = 'RHSSpring';
d.measFun     = 'MeasSpring';
d.measFunData = [];
d.alpha       = 1;
d.kappa       = 2;
d.beta        = 2;
d.dY          = 1;
d.dT          = dT;
d.rHSFunData  = dRHS;
d.rP          = 0.001;
d.rY          = sigY^2;
t             = 0;
y             = 0;
d.w           = dRHS.w/2;
d             = UKFP('initialize', d );
y             = MeasSpring(x) + sigY*randn;

for k = 1:nSim

  % Plotting
  %---------
	d.x     = x;
	xP(:,k) = [y; x; d.w;  d.p];

  % Update the RHS
  %---------------
  x       = RK4( 'RHSSpring', x, dT, 0, dRHS );

  % Measurement
  %------------
  y       = MeasSpring(x) + sigY*randn;
  t       = t + dT;

  % Kalman Filter
  %--------------
  d.t     = t;
  d       = UKFP( 'update', d, y );
end

t = (0:(nSim-1))*dT;
xL = {'Meas' 'x' 'v' 'Param' 'Covariance'};
Plot2D( t, xP, 'Time (sec)', xL, 'Nonlinear Spring Parameter estimation' );


%--------------------------------------
% $Date$
% $Id: b67c78dd74f52a70bc7c45c6fae04517579a6e3b $

Published with MATLAB® R2021b