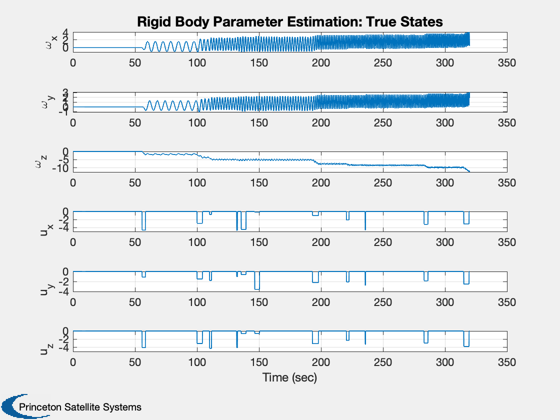
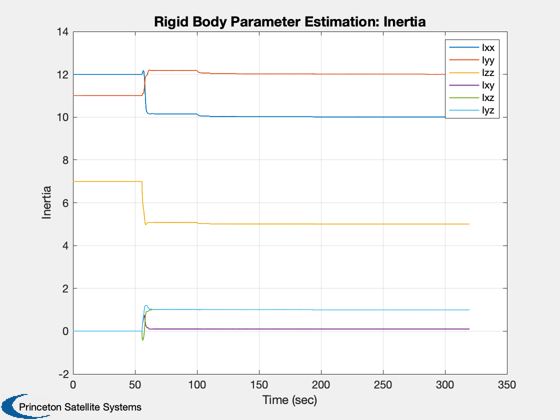
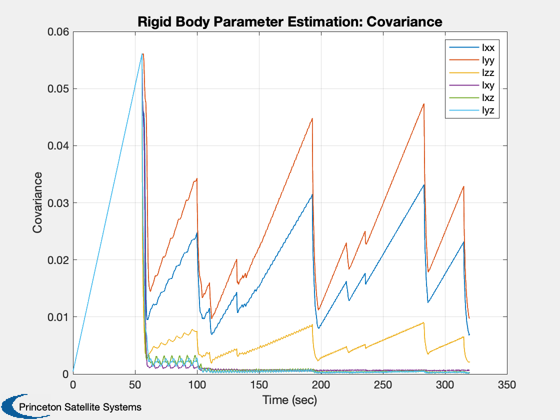
Demonstrate UKF parameter estimation with a rigid body.

This estimates only inertia. The parameter estimator does not estimate the body state. ------------------------------------------------------------------------- See also Plot2D, RK4, UKFP -------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------


nSim          = 3200;
dRHS          = struct;
dRHS.w        = [10 12 5 0.1 1 1];
sigY          = 0.0001;%0.05;
xP            = zeros(18,nSim);
x             = [0;0;0];
dT            = 0.1;
uType         = 'sine';

Estimation parameters

%----------------------
d.x           = x;
d.int         = 'RK4';
d.rHSFun      = 'RHSRBUKF';
d.measFun     = 'GXUKF';
d.measFunData = [];
d.alpha       = 1e-3;
d.kappa       = 0;
d.beta        = 2;
d.dT          = dT;
d.rHSFunData  = dRHS;
d.rY          = 0.00001*eye(3);
d.rP          = 0.0001*eye(6);
d.p           = 4*d.rP;
t             = 0;
y             = 0;
d.w           = [12 11 7 0 0 0]';
d             = UKFP('initialize', d );
tPulseStop    = 10;
dRHS.u        = [0;0;0];
uNext         = 0.1*(0.5*rand(3,1) - 0.5);
tNext         = t + 20*rand;

Run the simulation

%-------------------
for k = 1:nSim

  % Plotting
  %---------
  d.x            = x; % This must be before the propagation
  xP(:,k)        = [x; d.w; diag(d.p);dRHS.u];

  if( strcmp(uType,'Sine') )
    dRHS.u = 0.1*[sin(0.03*t);cos(0.02*t);sin(0.01*t)];
  else
    if( t >= tPulseStop )
      dRHS.u     = [0;0;0];
      uNext      = 10*(0.5*rand(3,1) - 0.5);
      tNext      = t + 50*rand;
      tPulseStop = 5*rand + tNext;
    elseif( t >= tNext )
      dRHS.u     = uNext;
    end
  end
  d.rHSFunData.u = dRHS.u;

  % Update the RHS
  %---------------
  x       = RK4( 'RHSRBUKF', x, dT, 0, dRHS );

  % Measurement
  %------------
  y       = x + sigY*randn(3,1);
  t       = t + dT;

  % Kalman Filter. This must be after the propagation
  %--------------------------------------------------
  d.t     = t;
  d       = UKFP( 'update', d, y );

end

t   = (0:(nSim-1))*dT;
yL  = {'\omega_x' '\omega_y' '\omega_z' 'u_x' 'u_y' 'u_z'};
leg = {'Ixx' 'Iyy' 'Izz' 'Ixy' 'Ixz' 'Iyz'};
Plot2D( t, xP( [1:3 16:18],:), 'Time (sec)', yL,      'Rigid Body Parameter Estimation: True States'     );
Plot2D( t, xP( 4: 9,:), 'Time (sec)', 'Inertia',    'Rigid Body Parameter Estimation: Inertia'    );
legend(leg{:})
Plot2D( t, xP(10:15,:), 'Time (sec)', 'Covariance', 'Rigid Body Parameter Estimation: Covariance' );
legend(leg{:})


%--------------------------------------
% $Date$
% $Id: b1f694c985bcd005f46ca3f1587307098b2fb32c $

Published with MATLAB® R2021b