Demonstrate simple dipole based momentum management

This uses a pseudo-inverse to get the best fit between the available
dipoles and the desired momentum unloading torque.

----------------------------------------------------------------------
See also Plot2D, TimeLabl, RK4, Date2JD, MomentumUnloading,
RHSMomentum, Period, BDipole
------------------------------------------------------------------------

Contents

%------------------------------------------------------------------------
%   Copyright (c) 2010 Princeton Satellite Systems, Inc.
%   All rights reserved.
%------------------------------------------------------------------------
%   Since version 9.
%------------------------------------------------------------------------

Simulation duration

%--------------------
tEnd  = 8000;

Time step

%----------
dT    = 1;
nSim  = ceil(tEnd/dT);

The momentum to be removed

%---------------------------
h    = [1;1;1];

Start Julian date

%------------------
d.jD0  = Date2JD([2012 4 5 0 0 0]);
xPlot  = zeros(9,nSim);

Momentum unloading gain

%------------------------
gain   = 0.01;

Orbit

%------
a      = 7000;
p      = Period(a);
theta  = linspace(0,2*pi*tEnd/p,nSim);
x      = a*[cos(theta);zeros(1,nSim);sin(theta)];

Run the simulation

%-------------------
t      = 0;

Dipole vectors

%---------------
u      = [1 0;0 1;0 0];

for k = 1:nSim

    % Magnetic field - the magnetometer output is proportional to this
    %-----------------------------------------------------------------
    b               = BDipole( x(:,k), d.jD0+t/86400 );

    [tMM, m, ang]	= MomentumUnloading( u, b, gain, h );

    % A time step with 4th order Runge-Kutta
    %---------------------------------------
    h               = RK4( @RHSMomentum, h, dT, t, tMM );

    xPlot(:,k+1)    = [h;m;b;ang*180/pi];
    t               = t + dT;

end

Plotting

%---------
[t, tL] = TimeLabl( (0:nSim)*dT );

Y-axis labels

%--------------
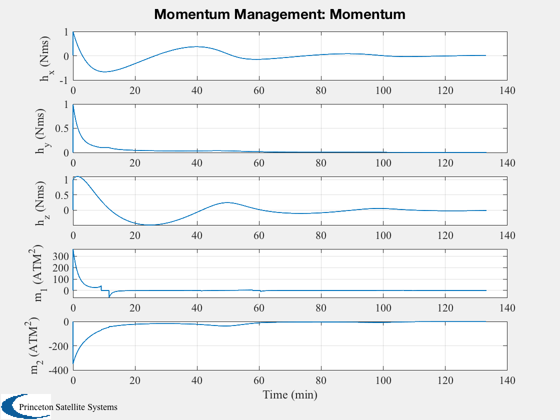
yL = {'h_x (Nms)' 'h_y (Nms)' 'h_z (Nms)' 'm_1 (ATM^2)' 'm_2 (ATM^2)'...
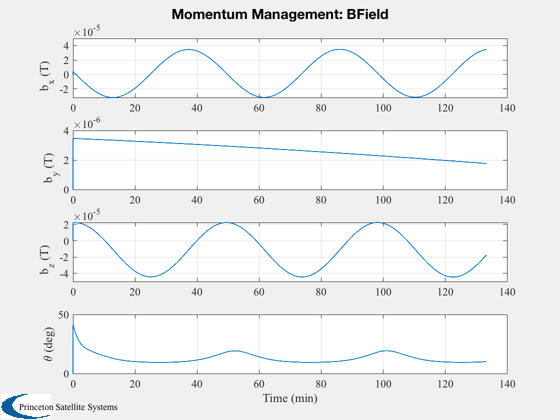
      'b_x (T)', 'b_y (T)' 'b_z (T)' '\theta (deg)'};

Plotting utility

%-----------------
Plot2D( t, xPlot(1:5,:), tL, yL(1:5), 'Momentum Management: Momentum' );
Plot2D( t, xPlot(6:9,:), tL, yL(6:9), 'Momentum Management: BField' );



%--------------------------------------

Published with MATLAB® R2019a