Continuous Stirred Tank Rector Startup Simulation

Simulates CSTR startup with an irreversible first order reaction. Goal is to produce propylene glycol (C).

Since version 1.
-------------------------------------------------------------------------
Reference: Fogler, H. S. (1999.) Elements of Chemical Reaction
           Engineering. pp. 554-557;
-------------------------------------------------------------------------
See also:    RHSFermenter, MuFermenter, TimeGUI, Plot2D
-------------------------------------------------------------------------

Model parameters
State
Number of sim steps
Plotting arrays
Run the simulation
Plot results

%--------------------------------------------------------------------------
%   Copyright (c) 2013 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Model parameters

-----------------

fA0   = 80;    % Flow lb-mol/h
fB0   = 1000;  % Flow lb-mol/h
fM0   = 100;   % Flow lb-mol/h
rhoA0 = 0.923; % Density lb-mol/ft^3
rhoB0 = 3.45;  % Density lb-mol/ft^3
rhoM0 = 1.54;  % Density lb-mol/ft^3

d.v0      = (fA0/rhoA0 + fB0/rhoB0 + fM0/rhoM0); % ft^3/h
d.hR      = -36000;    % Heat of reaction (But/lb-mol A)
d.v       = (1/7)*500; % Tank volume ft^3
d.cA0     = fA0/d.v0;  % Concentration of propylene oxide (lb-mol/ft^3)
d.cB0     = fB0/d.v0;  % Concentration of water  (lb-mol/ft^3)
d.cM0     = fM0/d.v0;  % Concentration of methanol  (lb-mol/ft^3)
d.cPA     = 35;        % Spec heat at constant pressure Btu/(lb-mol-deg F)
d.cPB     = 18;        % Spec heat at constant pressure Btu/(lb-mol-deg F)
d.cPC     = 46;        % Spec heat at constant pressure Btu/(lb-mol-deg F)
d.cPM     = 19.5;      % Spec heat at constant pressure Btu/(lb-mol-deg F)
d.tA1     = 60;        % Temperature at water inlet deg-F
d.fA0     = fA0;       % Flow lb-mol/h
d.T0      = 75;        % Initial temperature deg-F
d.uA      = 16000;     % Heat exchanger coefficient Btu/h deg-F
d.u       = 1000;      % Water flow (control) lb mol/h
d.thetaCP = d.cPA  + (d.cPB*fB0 + d.cPM*fM0)/fA0;  % Btu/(lb-mol-deg F)

State

[cA (lb-mol/ft^3); cB (lb-mol/ft^3); cC (lb-mol/ft^3); cM (lb-mol/ft^3); T (deg-F)] ------------------

x           = [0;3.45;0;0;75];
t           = 0;

Number of sim steps

--------------------

nSim        = 1000;
tEnd        = 4;
dT          = tEnd/nSim;
tEnd        = nSim*dT;

Plotting arrays

----------------

tPlot      = zeros(1,nSim);
xPlot      = zeros(5,nSim);

Run the simulation

See RHSCSTRStartup.m which models the startup of a CSTR. --------------------------------------------------------

for k = 1:nSim
  x           = RK4( 'RHSCSTRStartup', x, dT, t, d );
  t           = t + dT;
  tPlot(k)    = t;
  xPlot(:,k)  = x;
end

Plot results

-------------

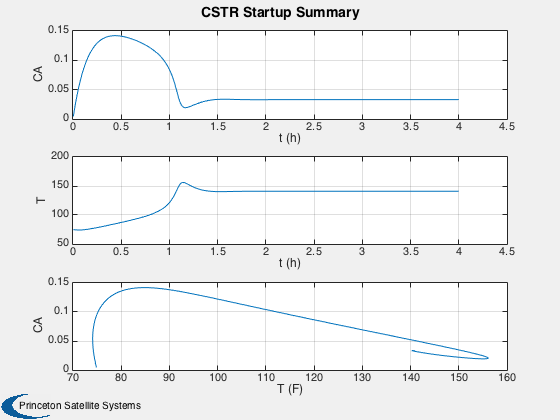
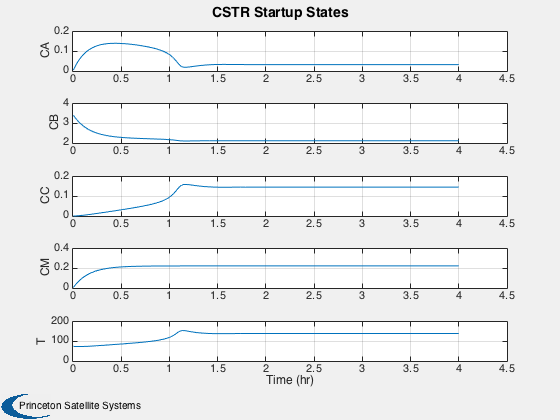
xL    = ['t (h)';'t (h)';'T (F)'];
Plot2D( [tPlot;tPlot;xPlot(5,:)], xPlot( [1 5 1],:),xL,['CA';'T ';'CA'],...
    'CSTR Startup Summary')
Plot2D( tPlot, xPlot,'Time (hr)',['CA';'CB';'CC';'CM';'T '],...
    'CSTR Startup States')

%--------------------------------------
% PSS internal file version information
%--------------------------------------