Continuous Fermenter with I/O Linearizing Control

Simulates a model of a continuous fermenter with an I/O linearizing control.

Since version 1.
-------------------------------------------------------------------------
Reference: Henson, M. A. and D. E. Seborg. (1997.) Nonlinear
           Process Control, Prentice-Hall. pp. 203-204.
-------------------------------------------------------------------------
See also:    RHSFermenter, MuFermenter, TimeGUI, Plot2D
-------------------------------------------------------------------------

Model parameters
State
Test
Controller
The control sampling period and the simulation integration time step
Number of sim steps
Plotting arrays
Run the simulation
Plot results

%--------------------------------------------------------------------------
%   Copyright (c) 2013 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Model parameters

-----------------

d.yXS   = 0.4;      % Cell-mass yield parameter (g/g)
d.beta  = 0.2;      % Yeild parameter (1/hr)
d.pM    = 50;       % Constant parameter (g/L)
d.kI    = 22;       % Constant parameter (g/L)
d.d     = 0.202;    % Dilution rate (1/hr)
d.alpha = 2.2;      % Yield parameter (g/g)
d.muM   = 0.48;     % Maximum specific growth rate (1/hr)
d.kM    = 1.2;      % Constant parameter (g/L)
d.sF    = 20;       % Feed substrate concentration (g/L)

State

[X;S;P] X = biomass concentration S = substrate concentration P = product concentration ---------------------------

x           = [6;5;19.14];
t           = 0;

Test

-----

d.muM       = 0.875*d.d;

Controller

-----------

epsilon      = 1;
ySP          = x(1);
dYInt        = 0;
v            = 0;
controllerOn = 0;

The control sampling period and the simulation integration time step

---------------------------------------------------------------------

dT          = 0.1;

Number of sim steps

--------------------

nSim        = 300;
tEnd        = nSim*dT;

Plotting arrays

----------------

tPlot      = zeros(1,nSim);
xPlot      = zeros(4,nSim);

Run the simulation

See RHSFermenter.m which gives a model of a constant volume reactor in which a single, rate limiting substrate promotes biomass growth and product formation. -------------------------------------------------------------------------

for k = 1:nSim

  % Controller
  %-----------
  if( controllerOn )

    dY    = ySP - x(1);
    v     = (2/epsilon)*dY + dYInt/epsilon^2;
    dYInt = dYInt + dT*dY;

    % Effectively this cancels the nonlinear term
    %--------------------------------------------
    u     = (v - MuFermenter( x, d )*x(1) )/(-x(1));

  else

	u     = 0;

  end

  d.d   = u;

  % Plotting
  %---------
  xPlot(:,k)  = [x;u];
  tPlot(k)    = t;


  x           = RK4( 'RHSFermenter', x, dT, t, d );
  t           = t + dT;


end

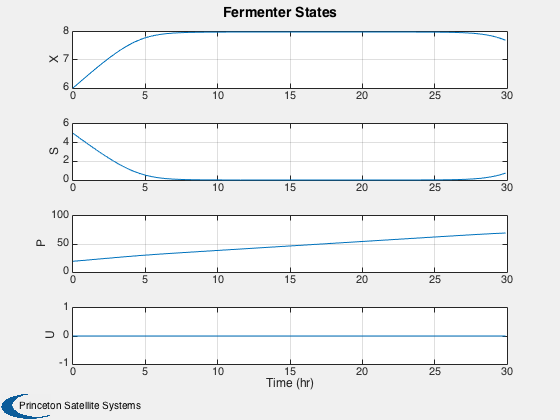
Plot results

%--------------
j     = 1:k;
Plot2D( tPlot, xPlot,'Time (hr)',['X';'S';'P';'U'],'Fermenter States')

%--------------------------------------
% PSS internal file version information
%--------------------------------------