Coarse probability demo

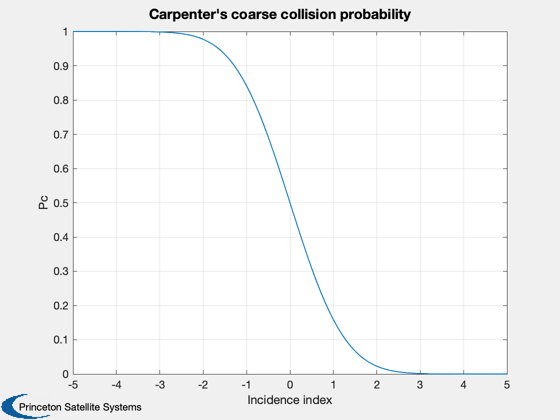
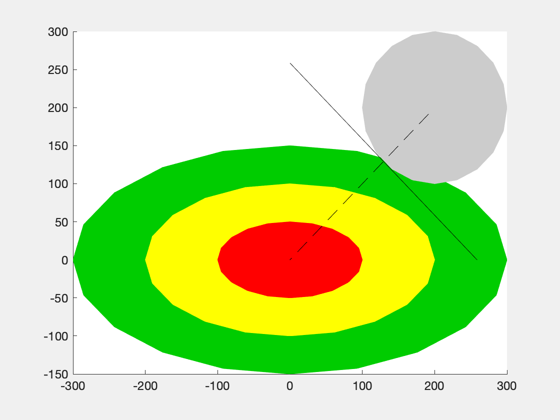
CoarseProp.m computes a collision probability estimate consisting of the integral outbound of the tangent between a circular avoidance region and the target's position probability density. The formulation is demonstrated using a set of plots to show the underlying probability function, the computation of the index and probabilityfor various realistic ratios of the collision parameters, and a visualization of the integral region.

Since version 7.
-------------------------------------------------------------------------
Reference: J. Russell Carpenter, 'Conservative Analytical Collision
Probability for Design of Orbital Formations', 2004
-------------------------------------------------------------------------

%--------------------------------------------------------------------------
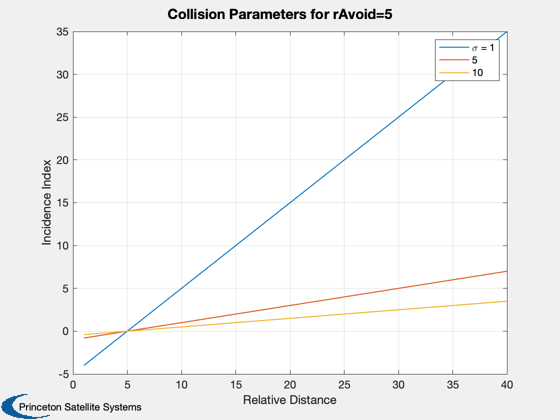
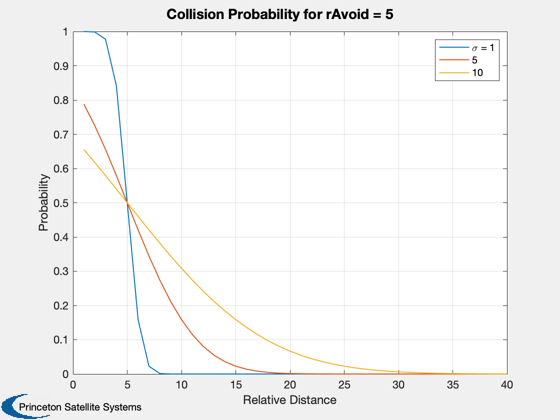
%   Copyright 2011 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

% The underlying probability function is based on erf
k = -5:0.1:5;
Pc = 0.5 - 0.5*erf(k/sqrt(2));
Plot2D(k,Pc,'Incidence index','Pc','Carpenter''s coarse collision probability');

% The incidence function
k = [];
dR = 1:40;
rAvoid = 5;
sigmaU = 1;
k(:,1) = (dR - rAvoid)/sigmaU;
sigmaU = 5; k(:,2) = (dR - rAvoid)/sigmaU;
sigmaU = 10; k(:,3) = (dR - rAvoid)/sigmaU;
Plot2D(dR,k,'Relative Distance','Incidence Index','Collision Parameters for rAvoid=5');
legend('\sigma = 1','5','10')

% Compute the probability for the same values
Pc = [];
for k = 1:length(dR)
  Pc(1,k) = CoarseProb( dR(k), rAvoid, 1);
  Pc(2,k) = CoarseProb( dR(k), rAvoid, 5);
  Pc(3,k) = CoarseProb( dR(k), rAvoid, 10);
end
Plot2D(dR,Pc,'Relative Distance','Probability','Collision Probability for rAvoid = 5');
legend('\sigma = 1','5','10')

rRel   = [200; 200];
sigma = diag([100 50]);
rAvoid = 100;
CoarseProb( rRel, rAvoid, sigma)

%--------------------------------------
% PSS internal file version information
%--------------------------------------

ans =
     0.010367

Published with MATLAB® R2020a