Simulation for testing the collision monitoring algorithms.

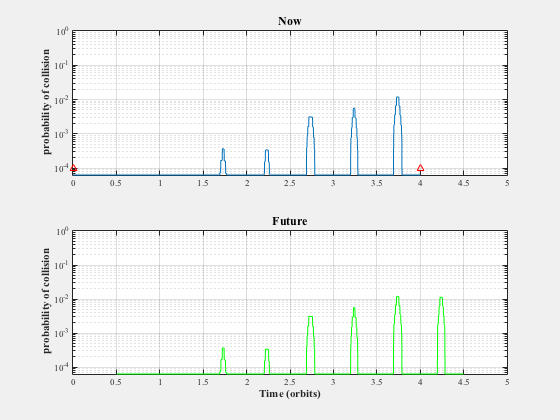
Computes the probability of collision between the two spacecraft for a fixed prediction window at each step. Also outputs the probability of collision for "now". Also simulates a fault in one of the spacecrafts in Projected Line formation (so no measurements are received for a fraction of an orbit) and plots the actual ("now") and predicted probability of collision over 2 orbits.

This demo does not include maneuvers for any of the spacecraft.

Since version 7.
------------------------------------------------------------------------
See also Constant, Plot2D, Plot3D, TimeLabl, Mag, UnwrapPhase,
CollisionMonitor, Plot3DEllipsoids, ProjLine, RotateState,
Geometry_Structure, HillsEqns, FFEccLawdensEqns, Goals2Hills, OrbRate,
M2Nu, Period
------------------------------------------------------------------------

Constants
Algorithm Initialization
Simulation Initialization
Generate SC positions
Initialize Matrices
Algorithm
Plot simulation results

%-------------------------------------------------------------------------------
%   Copyright (c) 2004-2005 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------


%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%% User Parameters %%%%%%%%%%%%%%%%%%

% Relative orbit selection
% 1: projected line with velocity set to cause a collision
% 2: Hills ellipse (Reference: Campbell IEE CST, 2005)
relOrbit = 2;

% Discrete or continuous propagation method
discreteProp = 0;

% Relative measurements (from monitoring spacecraft)
relativeMeas = 1;

% Time window for prediction
predictTime = 0.5;    % number of orbits
nSamples    = 2;

% Uncertainty in measurements of target, one sigma
positionError = 0.1;    % m
velocityError = 0.0005; % m/s

% Reference orbit eccentricity
eRef = 1e-6;

% Relative orbit characteristic distance (km)
dR = 0.05;

% Measurement fault times (orbits)
faultStart = 0;
faultEnd   = 2;

% Flag to plot the Hills orbit
plotFlag = 0;

% Index of sample times to save
nStore = 1;

%%%%%% End of Parameters %%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Constants

%--------------------------
deg2rad  = pi/180.0;  % radians to degrees
km2m     = 1.0e03;

Algorithm Initialization

%--------------------------

% Orbit parameters
d.hRef       = 550.0;	  % km - altitude of the reference orbit
d.eRef       = eRef;    % eccentricity
d.dR         = dR;       % km - distance between spacecrafts
d.initBounds = [positionError*[1 1 1] velocityError*[1 1 1]]; % 1 sig error in measurement (0.1m and 0.5mm/s)

% General
d.nSC          = 2;     % the number of S/C is a constant, two real S/C
                        % plus a "virtual" S/C at the formation center
d.predictTime  = predictTime*Period(Constant('earth radius mean')+d.hRef); % amount of time to predict for
d.nSampleTimes = nSamples; % number of sample times - must be at least 2
d.scalev       = 4;        % sigma for GPS measurement noise
d.discrete     = discreteProp;

% Spacecraft physical parameters
d.mSC   = 150;		      % kg - spacecraft mass
d.lenSC = 7.0;		      % m -  spacecraft length
d.diaSC = 4.0;		      % m -  spacecraft diameter
d.volSC = 4/3*pi*((d.lenSC/2)^3); % Assume sphere
d.Cd    = 2.2;			   % drag coefficient
d.Cr    = 1;            % reflectivity of s/c: 0.0 for translucent;
                        % 1.0 for black-body; 2.0 for flat mirror

Simulation Initialization

%---------------------------
nPtsPerOrbit = 500;	    % number of points at which to compute orbit data
jD           = 2451245;	% epoch in the Julian date system
aRef         = Constant('earth radius mean') + d.hRef;
incRef       = 85*deg2rad;	% inclination of reference orbit
orbPeriod    = Period(aRef);	% Orbit period (sec)
wn           = OrbRate(aRef);

Generate SC positions

%----------------------
switch relOrbit
  case 1
    % Projected Line with impending collision
    % Keplerian element set for each spacecraft orbit ([a,i,W,w,e,M])
    [elSet,rH0,vH0] = ProjLine( aRef, incRef, 2, d.dR );
    % Setting up a collision between the 2 satellites
    vH0(2,1) = d.dR/orbPeriod/3; % This velocity with ProjLine causes a collision in one orbit

    rH0 = km2m*rH0;
    vH0 = km2m*vH0;
    xH0_1 = [rH0(:,1);vH0(:,1)];
    xH0_2 = [rH0(:,2);vH0(:,2)];
    % number of orbits
    nOrbits = 2;
    iPlot = [1 2 3];
  case 2
    % Projected circle state
    g      = Geometry_Structure;
    phi    = [45 135]*deg2rad;
    g.aE   = d.dR;
    g.zLan = 0.0125*0;
    g.zInc = 0.0125*0;
    g1    = RotateState(g,phi(1));
    xH0_1 = km2m*Goals2Hills(wn,0,g1);
    g2    = RotateState(g,phi(2));
    xH0_2 = km2m*Goals2Hills(wn,0,g2);
    yAxis = [0 2*pi 0 80];
    % number of orbits
    nOrbits = 4;
    faultEnd = nOrbits;
    iPlot = [3 2 1];
end

% Time
nPts         = nPtsPerOrbit * nOrbits;
duration     = nOrbits * orbPeriod;
MET          = linspace(0, duration, nPts);
dTSim        = MET(2)-MET(1);
tFaultStart  = round(orbPeriod * faultStart);
tFaultEnd    = round(orbPeriod * faultEnd);

% Propagate in Hills frame
xHill = [];
nu0 = 0;
nuF = UnwrapPhase(M2Nu(eRef,wn*MET)+nu0);
xHill(:,:,1) = FFEccLawdensEqns( xH0_1, nu0, nuF, eRef, wn );
xHill(:,:,2) = FFEccLawdensEqns( xH0_2, nu0, nuF, eRef, wn );

if plotFlag
  % spacecraft orbits:
  h = Plot3D(xHill(iPlot,:,1),'z','y','x','Spacecraft Hills Orbits'); hold on;
  plot3(  xHill(iPlot(1),1,1),xHill(iPlot(2),1,1),xHill(iPlot(3),1,1),'b.','markersize',20);
  plot3(  xHill(iPlot(1),:,2),xHill(iPlot(2),:,2),xHill(iPlot(3),:,2),'r');
  plot3(  xHill(iPlot(1),1,2),xHill(iPlot(2),1,2),xHill(iPlot(3),1,2),'r.','markersize',20);
  axis equal;
  Plot2D( nuF, Mag(xHill(1:3,:,2)-xHill(1:3,:,1)) );
  if exist('yAxis')
    axis(yAxis);
  end
  return;
end

% scales time and generates labels for it
[tForPlots,tLabel] = TimeLabl(MET);

Initialize Matrices

%--------------------
Sigww = zeros(3,3,d.nSC-1);
Sigvv = zeros(6,6,d.nSC-1);
% arrays for storing set membership estimator results (only for the 2 real S/C)
xhat   = zeros(6,nPts,d.nSC-1);
Phat   = zeros(6,6,nPts,d.nSC-1);
prob   = zeros(d.nSampleTimes,nPts);
minD   = zeros(d.nSampleTimes,nPts);

Algorithm

%----------
hW = waitbar(0,'Collision Sim');
if relativeMeas
  CollisionMonitor('initialize',d,jD,[zeros(6,1) xH0_2-xH0_1] );
  xhat(:,1,2) = xH0_2-xH0_1;
else
  CollisionMonitor('initialize',d,jD,[xH0_1 xH0_2] );
  xhat(:,1,1) = xH0_1;
  xhat(:,1,2) = xH0_2;
end
tic;
for n = 2:nPts
	if( tFaultStart < MET(n) && MET(n) < tFaultEnd )
    % measurement failure!
    y = [];
  else
  % measurements, no noise added
  if relativeMeas
    y1 = [0;0;0;0;0;0];
    y2 = xHill(:,n,2) - xHill(:,n,1);
  else
    y1 = xHill(:,n,1);
    y2 = xHill(:,n,2);
  end
  y = [y1';y2']'; % GPS measurement at time n
	end
  [prob(:,n), minD(:,n), xhatT, PhatT] = CollisionMonitor( 'run', [], jD+MET(n)/86400, y );
  xhat(:,n,1) = xhatT(:,nStore,1);
  xhat(:,n,2) = xhatT(:,nStore,2);
  Phat(:,:,n,1) = PhatT(:,:,nStore,1);
  Phat(:,:,n,2) = PhatT(:,:,nStore,2);
  waitbar(n/nPts);
end
timeElapsed = toc;
DispWithTitle(timeElapsed,'Elapsed time');
close(hW)
if relativeMeas
  xHill(1:3,:,2) = xHill(1:3,:,1) - xHill(1:3,:,2);
  xHill(1:3,:,1) = xHill(1:3,:,1) - xHill(1:3,:,1);
  dNom = Mag(xHill(1:3,:,2));
else
  dNom = Mag(xHill(1:3,:,1) - xHill(1:3,:,2));
end

Elapsed time
       8.5162

Plot simulation results

%------------------------
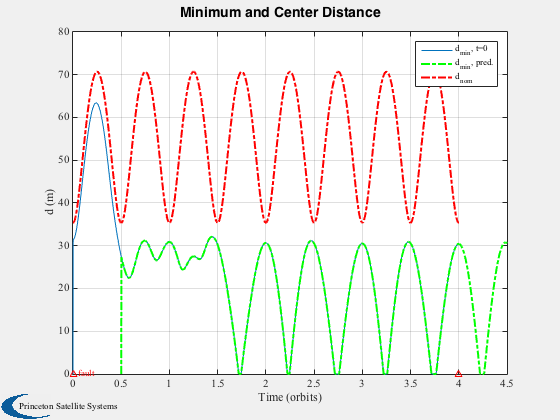
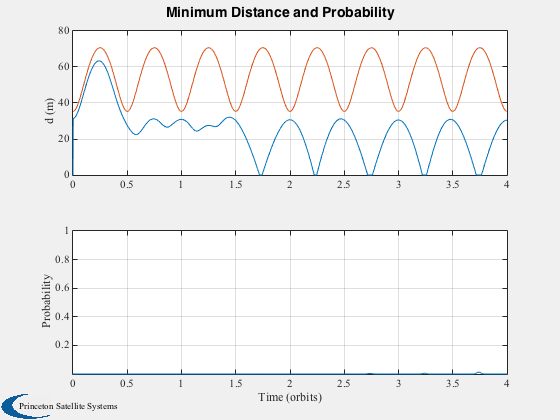
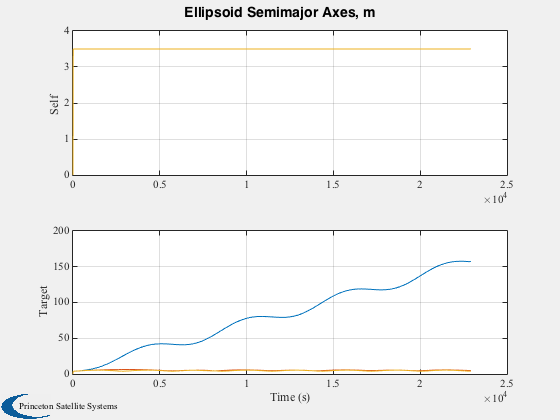
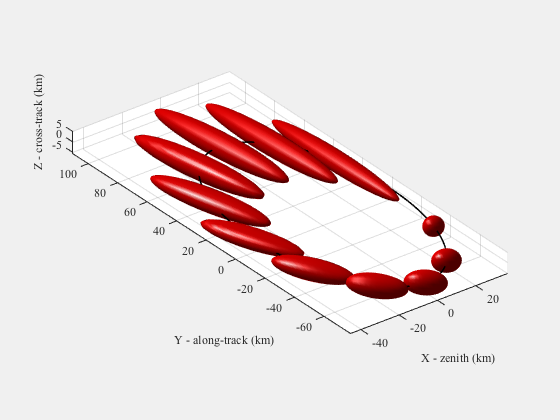
nPredictPts = round(d.predictTime/orbPeriod*nPtsPerOrbit);
METfuture   = linspace(0,duration+d.predictTime,nPts+nPredictPts)/orbPeriod;
z           = zeros(1,nPredictPts);

% Collision probability compared against prediction
figure('name','Prediction Performance');
subplot(2,1,1)
l = semilogy(MET/orbPeriod,prob(1,:));
set(l,'linewidth',1)
ylabel('probability of collision','fontweight','bold','fontsize',11)
grid on;
hold on
l = semilogy([tFaultStart tFaultEnd]/orbPeriod,[1 1]*1e-4,'r^');
set(l,'linewidth',1)
h = text(0,0,'fault');
set(h,'color',[1 0 0]);
axis([0 nOrbits+1 0 1]);
title('Now','fontweight','bold','fontsize',12);
subplot(2,1,2)
l = semilogy((MET+d.predictTime)/orbPeriod,prob(2,:),'g');
set(l,'linewidth',1)
ylabel('probability of collision','fontweight','bold','fontsize',11)
xlabel('Time (orbits)','fontweight','bold','fontsize',11)
title('Future','fontweight','bold','fontsize',12);
axis([0 nOrbits+1 0 1]);
grid on;

% Minimum distance
Plot2D(MET/orbPeriod,minD(1,:),'Time (orbits)','d (m)','Minimum and Center Distance');
hold on
plot((MET+d.predictTime)/orbPeriod,minD(2,:),'g-.','linewidth',2);
plot((MET)/orbPeriod,dNom,'r-.','linewidth',2);
legend('d_{min}, t=0','d_{min}, pred.','d_{nom}')
plot([tFaultStart tFaultEnd]/orbPeriod,[0 0],'r^')
h = text(0.05,0.05,'fault');
set(h,'color',[1 0 0])
grid on;

% Both metrics together for "now"
h = Plot2D(MET/orbPeriod,[minD(1,:);dNom;prob(1,:)],'Time (orbits)',{'d (m)','Probability'},...
  'Minimum Distance and Probability',{'lin' 'ylog'},['[1 2]';'[3]  ']);
axis([0 nOrbits 8e-6 1])

% View stored ellipsoids along their trajectory
%AnimateFunction('initialize',struct('xhat',xhat,'Shat',Phat,'c',{[0.7;0;0] [0;0.7;0]}),@PlotEllipsoids,MET/orbPeriod);

% Plot ellipsoid sizing
el1 = zeros(3,nPts);
el2 = zeros(3,nPts);
for k = 1:nPts
  P1 = Phat(1:3,1:3,k,1);
  P2 = Phat(1:3,1:3,k,2);
  [u,s,v]  = svd(P1);
  el1(:,k) = sqrt(diag(s));
  [u,s,v]  = svd(P2);
  el2(:,k) = sqrt(diag(s));
end
Plot2D(MET,[el1;el2],'Time (s)',{'Self','Target'},'Ellipsoid Semimajor Axes, m','lin',...
  ['[1 2 3]';'[4 5 6]'])
Plot3DEllipsoids( xhat(1:3,1:nPtsPerOrbit,2), Phat(1:3,1:3,1:nPtsPerOrbit,2),12 )

% Compare against Monte-Carlo simulation using HillsEqns
if relOrbit == 2
  tMean    = 3.75;
else
  tMean    = 1;
end
tCollide = linspace(tMean-0.1,tMean+0.1,25)*orbPeriod;
nProp = 2000;
y0 = xH0_2-xH0_1;
dMin = zeros(1,nProp);
for k = 1:nProp
  y = y0 + d.initBounds'.*randn(6,1);
  xHmc = HillsEqns( y, wn, tCollide, 1 );
  dMin(k) = min(Mag(xHmc(1:3,:)));
end
probTrue = length(find(dMin<d.lenSC))/nProp;
fprintf(1,'True probability of collision at %2.2g orbits: %3.3g%%\n',tMean,probTrue*100);


%--------------------------------------
% PSS internal file version information
%--------------------------------------

True probability of collision at 3.8 orbits: 2.35%