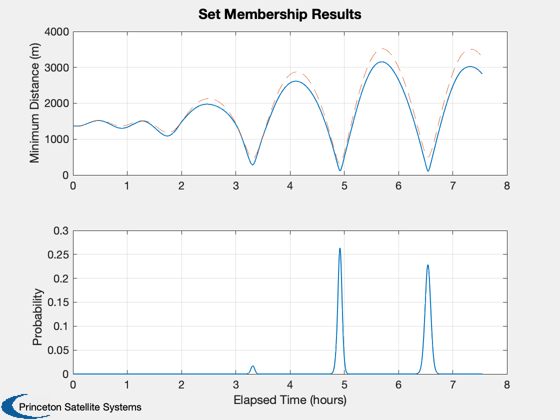
Collision monitoring demo.

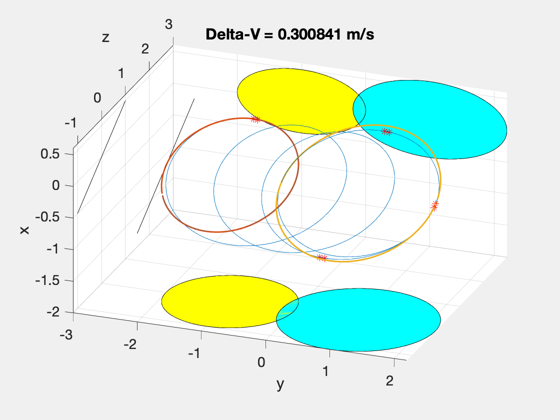
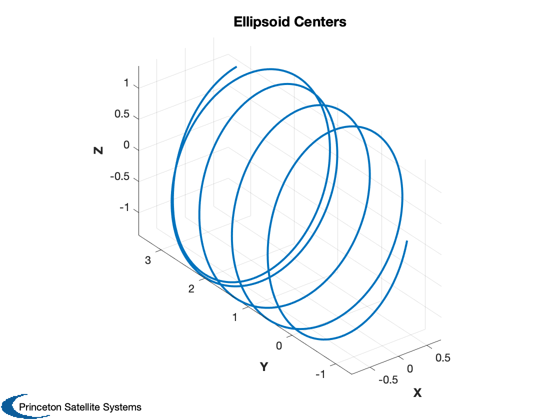
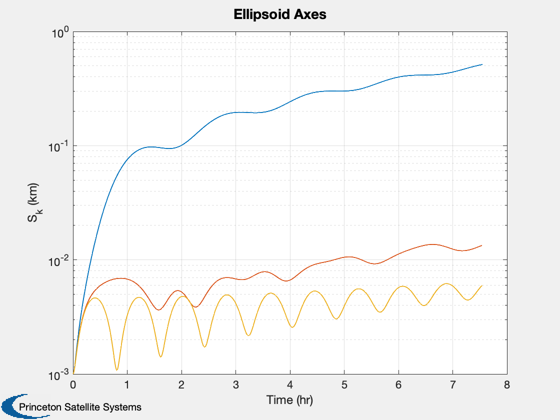
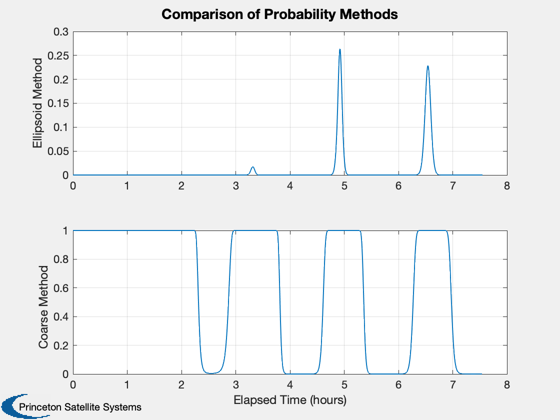
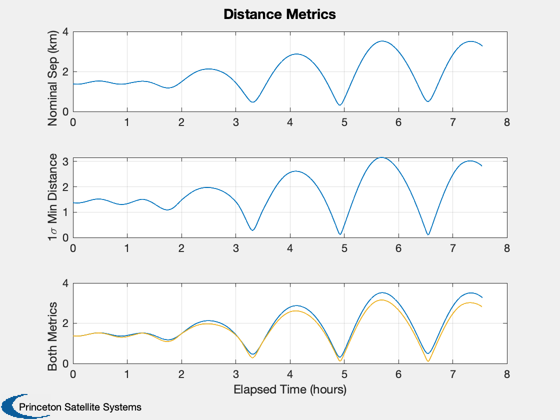
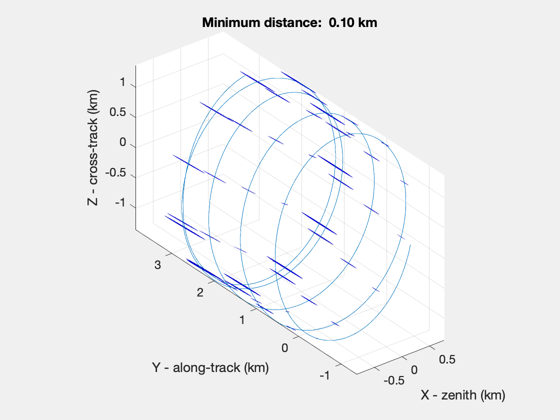
Compare CollisionSurvey and coarse methods. Note how the ellipsoids lengthen along-track over the propagation.

Since version 7.

%-------------------------------------------------------------------------------

%-------------------------------------------------------------------------------
%  Copyright 2005 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

% Setup plausible conditions
[dColl, y, mvr1, mvr2]  = CollisionInit(1);

% Increase the initial error so we can see results on the scale of the
% trajectory
dColl.S0 = 100*dColl.S0;

% 3-sigma ellipsoids
d.scalev = 3;
disp('First calculate 3-sigma distances and probabilities...')
tic
[prob, dMin, xhat, Shat, tProp] = CollisionSurvey(dColl,0,[y(:,2)-y(:,1)],mvr1,mvr2);
toc
% plot algorithm results
Plot2D([tProp-tProp(1)]/3600,[1000*cell2mat(dMin);cell2mat(prob)],'Elapsed Time (hours)',...
  char({'Minimum Distance (m)','Probability'}),'Set Membership Results');
subplot(2,1,1); hold on;
plot([tProp-tProp(1)]/3600,1000*Mag(xhat{1}(1:3,:)),'--')
Plot3D(xhat{1}(1:3,:),'X','Y','Z','Ellipsoid Centers');  axis equal; view(3)
S = zeros(3,length(tProp));
for k = 1:length(tProp)
  S(:,k) = sqrt(svd(Shat{1}(1:3,1:3,k)));
end
Plot2D(tProp/3600,S,'Time (hr)','S_{k} (km)','Ellipsoid Axes','ylog');

%-------------------------------------------
% Comparison to Carpenter's 'coarse' method
%-------------------------------------------

% 1-sigma ellipsoids
d.scalev = 1;
disp('Calculate 1-sigma ellipsoids...')
[prob1, dMin1, xhat1, Shat1, tProp1] = CollisionSurvey(dColl,0,[y(:,2)-y(:,1)],mvr1,mvr2);
xHill = {};
nu0      = M2NuAbs(dColl.eRef,dColl.MRef);
nuF      = M2NuAbs(dColl.eRef,dColl.MRef+dColl.rate*tProp);
xHill{1} = FFEccLawdensEqns( y(:,1), nu0, nuF, dColl.eRef, dColl.rate );
xHill{2} = xhat1{1};

% coarse probability
disp('Coarse probability method, using ellipsoids...');
[r0,v0] = RVFromKepler(dColl.el0,tProp-tProp(1));
xInertial = zeros(size(xhat1{1}));
SInertial = zeros(size(Shat1{1}));
rRel = zeros(1,length(tProp));
SConj = zeros(3,3,length(tProp),2);
for k = 1:length(tProp)
  [A, Adot] = GetHillsMats( r0(:,k), v0(:,k) );
  Bhe = inv([A zeros(3,3); Adot A]);
  for n = 1:2
    xInertial(:,k,n) = Bhe*xHill{n}(:,k);
    SInertial(:,:,k,n) = Bhe*Shat1{1}(:,:,k)*Bhe';
  end
end
probC = zeros(1,length(tProp));
for k = 1:length(tProp)
  % transform to conjunction plane
  xRel = xInertial(:,k,2) - xInertial(:,k,1);
  rRel = Mag(xRel(1:3));
  C = ConjunctionPlane( xRel );
  SConj1 = C'*SInertial(1:3,1:3,k,1)*C;
  SConj2 = C'*SInertial(1:3,1:3,k,2)*C;
  beta = 1/(1+sqrt(trace(SConj1)/trace(SConj2)));
  Se   = SConj1/(1-beta) + SConj2/beta;
  Se   = SConj2;
  % compute probability
  rAvoid = dColl.lenSC/2;
  sigmaU = sqrt(SConj2(1,1));
  probC(k) = CoarseProb(rRel,rAvoid,sigmaU);
end

% Plot results of the two methods
tPlot = [tProp-tProp(1)]/3600;
Plot2D(tPlot,[prob{1};probC],'Elapsed Time (hours)',...
  char({'Ellipsoid Method','Coarse Method'}),'Comparison of Probability Methods');
dNom = Mag(xhat1{1}(1:3,:));
Plot2D(tPlot,[dNom;dMin1{1};dMin{1}],'Elapsed Time (hours)',...
  char({'Nominal Sep (km)','1\sigma Min Distance','Both Metrics'}),'Distance Metrics','lin',['[1]    ';'[2]    ';'[1 2 3]']);
subplot(3,1,1)
[dNomM,iMin] = min(dNom);
text(tPlot(iMin)+0.2,70,sprintf('d_{min} = %5.1f',dNomM));
subplot(3,1,2)
[dMinM,iMin] = min(dMin1{1});
text(tPlot(iMin)+0.2,70,sprintf('d_{min} = %5.1f',dMinM));

% 3D Plotting of ellipsoids
ViewEllipsoid( xhat, Shat, dMin )

%--------------------------------------
% PSS internal file version information
%--------------------------------------

First calculate 3-sigma distances and probabilities...
Elapsed time is 0.189920 seconds.
Calculate 1-sigma ellipsoids...
Coarse probability method, using ellipsoids...

Published with MATLAB® R2020a