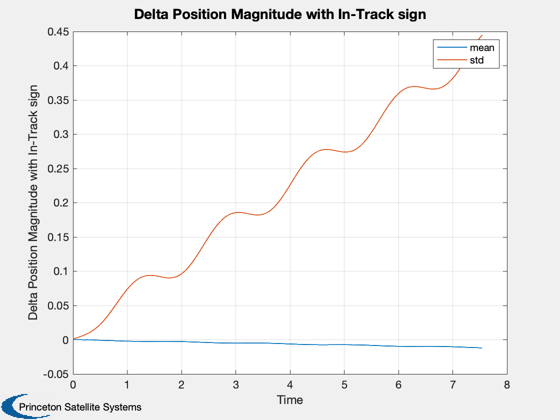
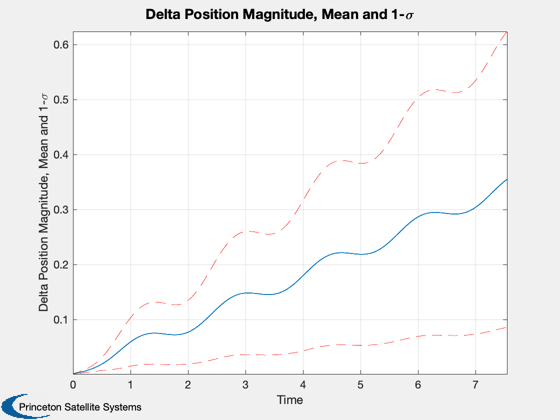
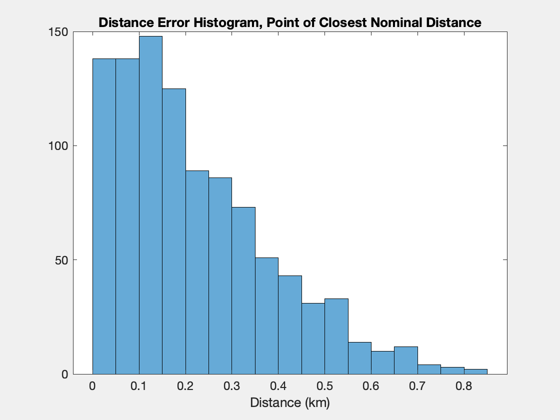
Collision monitoring demo: compare CollisionSurvey and coarse methods.

------------------------------------------------------------------------
References:
J. Russell Carpenter, "Conservative Analytical Collision Probability for
Design of Orbital Formations", Goddard Space Flight Center, 2004.
Mark Campbell, "Collision Monitoring Within Satellite Clusters", IEEE
TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY, VOL. 13, NO. 1, JANUARY 2005
------------------------------------------------------------------------
See also Plot2D, Plot3D, IntersectLineAndEllipsoid, Mag, Unit,
CoarseProb, CollisionInit, CollisionMonteCarlo, CollisionSurvey,
VerifyCollStruct, FFEccLawdensEqns, ManeuverStruct2AccelVector, M2NuAbs
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright 2005 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------
%   Since version 7.
%-------------------------------------------------------------------------------

% Setup plausible conditions
[dColl, y, mvr1, mvr2]  = CollisionInit(1);
dColl.initBounds = dColl.initBounds*10; % optional, adjust initial uncertainty
dColl = VerifyCollStruct( dColl );

% 4-sigma ellipsoids
dColl.scalev = 4;
dColl = VerifyCollStruct( dColl );
disp('First calculate 4-sigma distances and probabilities...')
tic
[prob, dMin, xhat, Shat, tProp] = CollisionSurvey(dColl,0,[y(:,2)-y(:,1)],mvr1,mvr2);
toc
% propagate Hills state of self
nu0 = M2NuAbs(dColl.eRef,dColl.MRef);
nuF = M2NuAbs(dColl.eRef,dColl.MRef+dColl.rate*tProp);
xH1 = FFEccLawdensEqns( y(:,1), nu0, nuF, dColl.eRef, dColl.rate );

% plot algorithm results
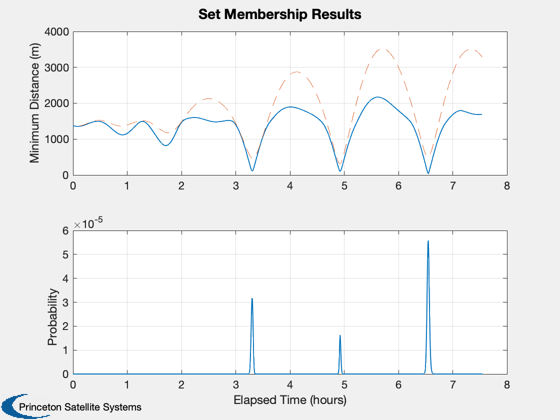
Plot2D([tProp-tProp(1)]/3600,[1000*cell2mat(dMin);cell2mat(prob)],'Elapsed Time (hours)',...
  char({'Minimum Distance (m)','Probability'}),'Set Membership Results');
subplot(2,1,1); hold on;
plot([tProp-tProp(1)]/3600,1000*Mag(xhat{1}(1:3,:)),'--')
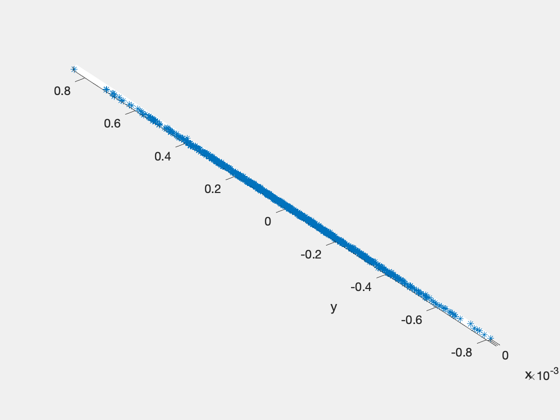
xhatA{1} = xhat{1} + xH1;
xhatA{2} = xH1;
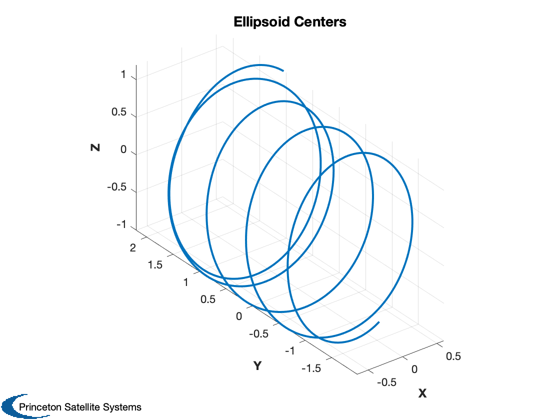
Plot3D(xhatA{1}(1:3,:),'X','Y','Z','Ellipsoid Centers');  axis equal; view(3)
Shat{2} = repmat(diag([1 1 1]*(dColl.lenSC/1000)^2),[1,1,length(tProp)]);
%AnimateFunction('initialize',struct('xhat',xhat,'Shat',Shat,'c',{[0.7;0;0] [0;0.7;0]}),@AnimateEllipsoids,tProp);
S = zeros(3,length(tProp));
for k = 1:length(tProp)
  S(:,k) = sqrt(svd(Shat{1}(1:3,1:3,k)));
end
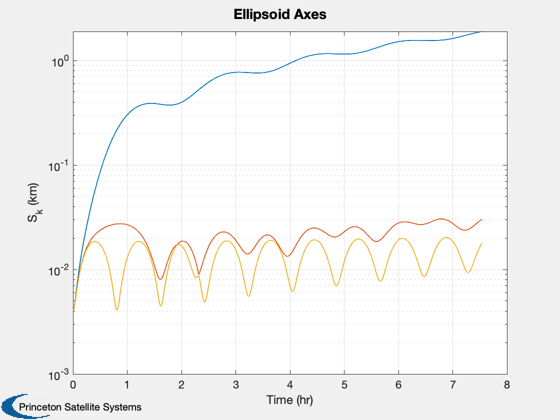
Plot2D(tProp/3600,S,'Time (hr)','S_{k} (km)','Ellipsoid Axes','ylog');

%-------------------------------------------

First calculate 4-sigma distances and probabilities...
Elapsed time is 0.142613 seconds.

Comparison to Carpenter's 'coarse' method

%-------------------------------------------

% 1-sigma ellipsoids
dColl.scalev = 1;
dColl = VerifyCollStruct( dColl );
disp('Calculate 1-sigma ellipsoids...')
[prob1, dMin1, xhat1, Shat1, tProp1] = CollisionSurvey(dColl,0,[y(:,2)-y(:,1)],mvr1,mvr2);

% coarse probability
disp('Coarse probability method, using ellipsoids...');
probC  = zeros(1,length(tProp));
rAvoid = dColl.lenSC/2/1000;
for k = 1:length(tProp)
  [u, s]    = svd(Shat1{1}(1:3,1:3,k));
  yI        = IntersectLineAndEllipsoid( [0;0;0], u'*Unit(-xhat1{1}(1:3,k)), sqrt(diag(s)) );
  sigmaU    = Mag(yI);
  probC(k)  = CoarseProb(Mag(xhat1{1}(1:3,k)),rAvoid,sigmaU+rAvoid);
end

Calculate 1-sigma ellipsoids...
Coarse probability method, using ellipsoids...

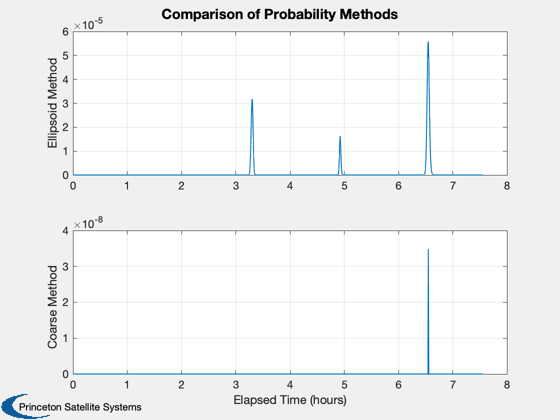
Plot results of the two methods

%--------------------------------
tPlot = [tProp-tProp(1)]/3600;
Plot2D(tPlot,[prob{1};probC],'Elapsed Time (hours)',...
  char({'Ellipsoid Method','Coarse Method'}),'Comparison of Probability Methods');
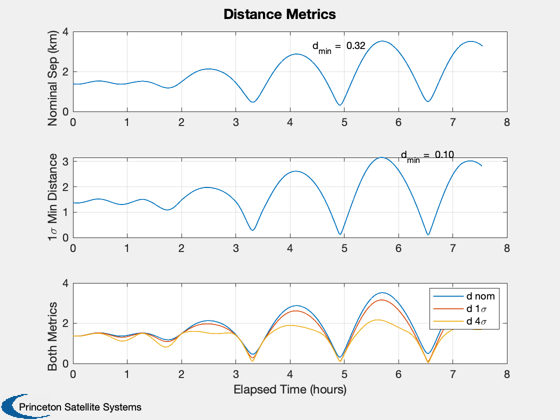
dNom = Mag(xhat1{1}(1:3,:));
Plot2D(tPlot,[dNom;dMin1{1};dMin{1}],'Elapsed Time (hours)',...
  char({'Nominal Sep (km)','1\sigma Min Distance','Both Metrics'}),...
  'Distance Metrics','lin',{1,2,[1 2 3]});
legend('d nom','d 1\sigma','d 4\sigma')
subplot(3,1,1)
[dNomM,iMin] = min(dNom);
text(tPlot(iMin)-0.5,3.2,sprintf('d_{min} = %5.2f',dNomM));
subplot(3,1,2)
[dMinM,iMin] = min(dMin1{1});
text(tPlot(iMin)-0.5,3.2,sprintf('d_{min} = %5.2f',dMinM));

% Monte-Carlo simulations for 'actual' probability of collision
%--------------------------------------------------------------
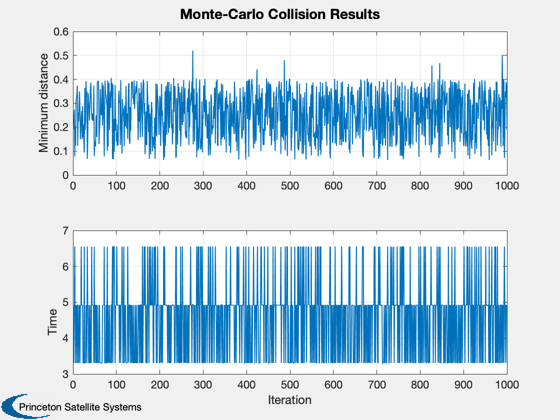
disp('Monte-Carlo simulations using CollisionMonteCarlo');
M   = dColl.MRef+dColl.rate*tProp;
aC2 = ManeuverStruct2AccelVector( mvr2, tProp );
[prob,dMin,tMin,drH] = CollisionMonteCarlo( dColl, y(:,2)-y(:,1), aC2, tProp, M );



%--------------------------------------

Monte-Carlo simulations using CollisionMonteCarlo
Generate matrices...
Propagate...
    50
   100
   150
   200
   250
   300
   350
   400
   450
   500
   550
   600
   650
   700
   750
   800
   850
   900
   950
        1000
Probability of collision:
     0

Published with MATLAB® R2020a