Collision monitoring demo for highly eccentric reconfiguration.

Used to produce a tetrahedron at apogee. Computes maneuvers and conducts collision survey.

Since version 7.
------------------------------------------------------------------------
See also AC, Plot2D, Plot3D, Mag, CollisionMonteCarlo, CollisionSurvey,
VerifyCollStruct, EccGeometry_Structure, DiscreteGVE,
FFEccTetrahedronGeometry, LPEccentricGVE, DeltaElem2Hills,
FFEccGoals2Hills, FFEccHills2DeltaElem, AccelVector2ManeuverStruct,
OrbRate, Nu2M, Nu2MAbs
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%  Copyright 2005 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

%%%%%%%% INPUT DATA HERE %%%%%%%%%%%%%%%%
% apogee and perigee of MMS-type orbit
Re = 6378.14;
apg = 18*Re;
prg = 1.2*Re;

% initial true anomaly
nu0 = 0;
nuF = pi;  % final true anomaly

% Number of steps for planning
nS  = 1500;

% size and orientation of desired tetrahedron
dR  = 1; % km
eul = [1.457142857;0;0];

% Monte-Carlo
doMC = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%-------------------------------

Reconfiguration Planning

%-------------------------------
trajFlag = 1;

% reference orbit
clear d
d.eRef = (apg/prg-1)/(apg/prg+1);
aRef   = apg/(1+d.eRef);
d.hRef = aRef - Re;
d.rate = OrbRate(aRef);
d.MRef = Nu2M(d.eRef,nu0);
MF     = Nu2MAbs(d.eRef,nuF);
d.el0  = [aRef,pi/6,0,0,d.eRef,d.MRef];
elF    = [d.el0(1:5),MF];
%elA    = El2Alfriend(d.el0);
d.dR   = dR;

% initial relative state for leader-follower
gInit = EccGeometry_Structure;
xH0   = zeros(6,3);
dEl0  = zeros(3,6);
for i=1:3,
   gInit.y0  = i;
   xH0(:,i)  = FFEccGoals2Hills( d.eRef, nu0, gInit, d.rate );
   dEl0(i,:) = FFEccHills2DeltaElem( d.el0, xH0(:,i), 2 );
end

% compute geometric goals for a repeating tetrahedron at apogee
gFinal = FFEccTetrahedronGeometry( pi, dR, eul );

% compute the target Hills-frame states
xHF = zeros(6,3);
for i=1:3
   xHF(:,i) = FFEccGoals2Hills( d.eRef, nuF, gFinal(i), d.rate );
   dElF(i,:) = FFEccHills2DeltaElem( elF, xHF(:,i), 2 );
end

accNom = (1e-3)/100; % nominal acceleration [km/s/s] (assume 1 Newton thruster, 100 kg spacecraft)

% plan maneuvers for each of the 3 relative spacecraft
disp('Planning 3 maneuvers...');
xHs  = cell(1,3);
aC   = cell(1,3);
t    = cell(1,3);
dEls = cell(1,3);
M    = cell(1,3);
for i=1:3
   [aC{i},t{i},flag] = LPEccentricGVE( d.el0, dEl0(i,:)', dElF(i,:)', MF, nS );
   mvr(i) = AccelVector2ManeuverStruct( aC{i}, t{i}, 0, accNom, 0 );
   fprintf('Maneuver %d of 3 complete...\n',i);
   %[aCT{i}] = ManeuverStruct2AccelVector( mvr(i), t{i} );
   if trajFlag
     [dEls{i},M{i}] = DiscreteGVE( d.el0, dEl0(i,:), aC{i}, t{i} );
     %xHs{i} = DeltaElem2HillsAlfriend( d.el0, dEls{i}, M{i} );
     xHs{i} = DeltaElem2Hills( d.el0, dEls{i} );
   end
end

% one-sigma measurement noise
d.initBounds   = [0.1 0.1 0.1 0.0005 0.0005 0.0005]/1000; % km, km/s
d.scalev       = 1;
d.mSC          = 100;
d.lenSC        = 7; % m
d.diaSC        = 1;
d.Cd           = 2;
d.Cr           = 1.5;

%-------------------------------

Planning 3 maneuvers...
Maneuver 1 of 3 complete...
Maneuver 2 of 3 complete...
Maneuver 3 of 3 complete...

Collision Monitoring

%-------------------------------

dColl = d;
mvr1  = [];
mvr2  = mvr;
% Testing:
% for k = 1:length(t)
%   mvr2(k).aC = aC{k};
%   mvr2(k).t = t{k};
% end

% 3-sigma ellipsoids
dColl.scalev = 4;
dColl        = VerifyCollStruct( dColl );
disp('Checking trajectories for collisions...')
tic
[prob, dMin, xhat, Shat, tProp] = CollisionSurvey(dColl,0,xH0,mvr1,mvr2);
toc
disp('Finished.')

%----------------------

Checking trajectories for collisions...
Elapsed time is 0.162806 seconds.
Finished.

Plotting

%----------------------
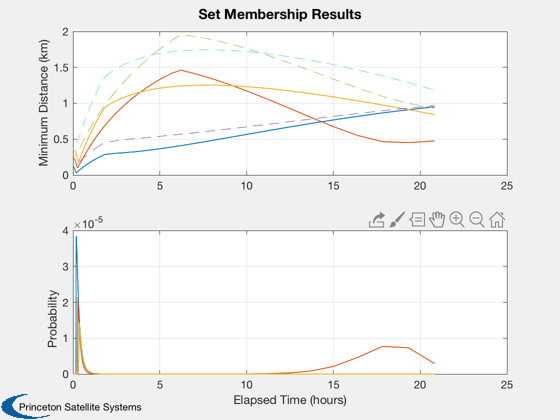
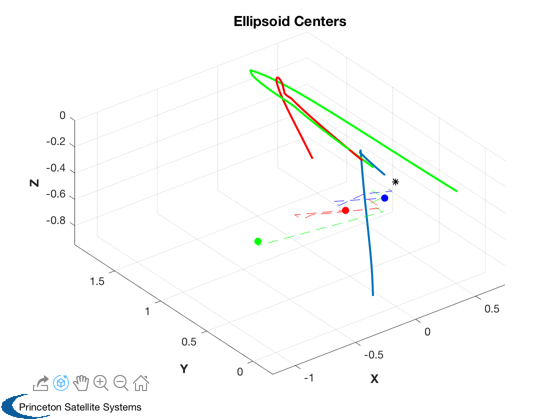
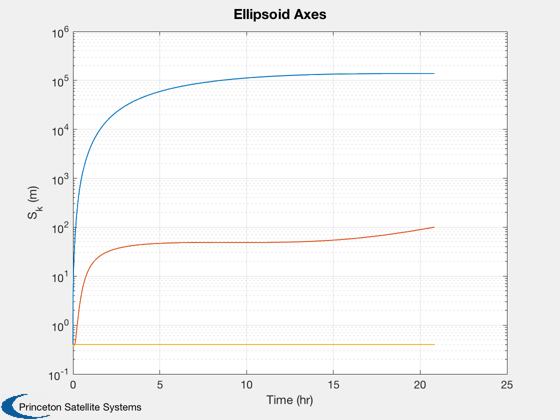
% Collision monitoring outputs
Plot2D([tProp-tProp(1)]/3600,[cell2mat(dMin);cell2mat(prob)],'Elapsed Time (hours)',...
  char({'Minimum Distance (km)','Probability'}),'Set Membership Results','lin',...
  ['[1 2 3]';'[4 5 6]']);
subplot(2,1,1); hold on;
dHPlot = [Mag(xhat{1}(1:3,:));Mag(xhat{2}(1:3,:));Mag(xhat{3}(1:3,:))];
plot([tProp-tProp(1)]/3600,dHPlot,'--')
% Trajectories
Plot3D(xhat{1}(1:3,:),'X','Y','Z','Ellipsoid Centers'); hold on;
plot3(0,0,0,'k*');
plot3(xhat{2}(1,:),xhat{2}(2,:),xhat{2}(3,:),'g','linewidth',2);
plot3(xhat{3}(1,:),xhat{3}(2,:),xhat{3}(3,:),'r','linewidth',2);
plot3(xHs{1}(1,:),xHs{1}(2,:),xHs{1}(3,:),'b--');
plot3(xHs{2}(1,:),xHs{2}(2,:),xHs{2}(3,:),'g--');
plot3(xHs{3}(1,:),xHs{3}(2,:),xHs{3}(3,:),'r--');
plot3(xHs{1}(1,end),xHs{1}(2,end),xHs{1}(3,end),'b.','markersize',20);
plot3(xHs{2}(1,end),xHs{2}(2,end),xHs{2}(3,end),'g.','markersize',20);
plot3(xHs{3}(1,end),xHs{3}(2,end),xHs{3}(3,end),'r.','markersize',20);
axis equal; view(3)
% Ellipsoids
%AnimateFunction('initialize',struct('xhat',xhat,'Shat',Shat,'c',...
%   {[0.7;0;0];[0;0.7;0];[0;0;0.7]}),@AnimateEllipsoids,tProp/3600);
S = zeros(3,length(tProp));
for k = 1:length(tProp)
  S(:,k) = sqrt(svd(Shat{1}(1:3,1:3,k)))*1000;
end
Plot2D(tProp/3600,S,'Time (hr)','S_{k} (m)','Ellipsoid Axes','ylog');

% Monte-Carlo for 3rd spacecraft (closest nominal pass)
if doMC
  disp('Perform Monte-Carlo simulations.');
  [probMC,dMinMC,tMin,drH] = CollisionMonteCarlo( dColl, xH0(:,3), aC{3}, t{3}, M{3} );
  fprintf('True probability of collision: %3.3g%%\n',probMC*100);
end


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2019a