Simulate relative motion in a HEO orbit with solar pressure disturbance

Since version 7.
-------------------------------------------------------------------------
See also Constant, Date2JD, DiscreteGVE, FFEccDeltaElem2Hills,
Hills2Frenet, OrbRate, M2NuAbs, Period, SunV1
-------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2005,2012 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Initialize simulation parameters:

jD0 = Date2JD;
nOrbits = 4;
mass = 1;
area = 1;
dEl0 = zeros(1,6);
%       a      i    W  w   e   M
el0 = [83500, pi/4, 0, 0, 0.8, 0];


disp('SETTING UP the simulation.')

SETTING UP the simulation.

SOLAR PRESSURE at 1 AU

Note: this is equivalent to solar flux / speed of light, or 1.367 / (3e8)

solarPressure    = Constant('solar pressure mks')*1e-3;  % kN/m^2

orbital parameters

a = el0(1);
n = OrbRate(a);
T = Period(a);
e = el0(5);

time

nSPO = 100; % number of samples per orbit
t = linspace(0,nOrbits*T,round(nSPO*nOrbits));  % time vector in seconds
jD = jD0 + t/86400;  % time vector in Julian Dates

compute direction of sun in ECI coordinates

[r,v] = RVOrbGen(el0,t);
unitSun = SunV1( jD, r );

compute accelaration due to solar pressure

disp('COMPUTING acceleration due to solar pressure.')
accSP = solarPressure*area/mass*unitSun;    % km/s/s

COMPUTING acceleration due to solar pressure.

Rotate to radial/along-track/cross-track (Hills) frame

accSPHills = zeros(size(accSP));
for i=1:length(t)
  m = GetHillsMats(r(:,i),v(:,i));
  accSPHills(:,i) = m*accSP(:,i);
end

simulate the dynamics in the relative frame

disp('RUNNING SIMULATION in relative frame using Gauss Variational Equations...')
[dEl,M] = DiscreteGVE( el0, dEl0, accSPHills(:,1:end-1), t );

RUNNING SIMULATION in relative frame using Gauss Variational Equations...

compute the Hills frame position and velocity

disp('COMPUTING the Hills frame state from the orbital element differencs.')
xH = zeros(size(dEl))';
for i=1:size(xH,2)
   xH(:,i) = FFEccDeltaElem2Hills( [el0(1:5),M(i)], dEl(i,:), 2 );
end

COMPUTING the Hills frame state from the orbital element differencs.

compute the Frenet frame position and velocity

disp('COMPUTING the Frenet frame state from the Hills frame state.')
nu = M2NuAbs( e, M );
xF = Hills2Frenet( xH, e, nu, n );

COMPUTING the Frenet frame state from the Hills frame state.

store results

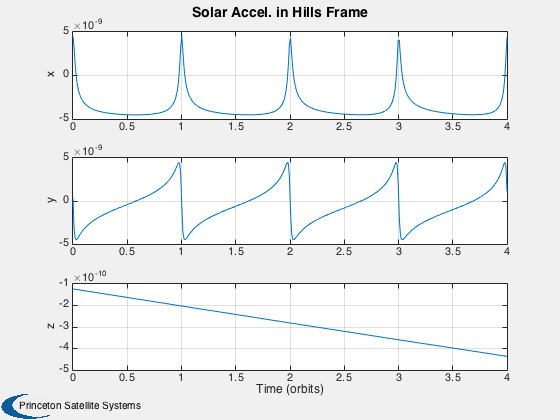
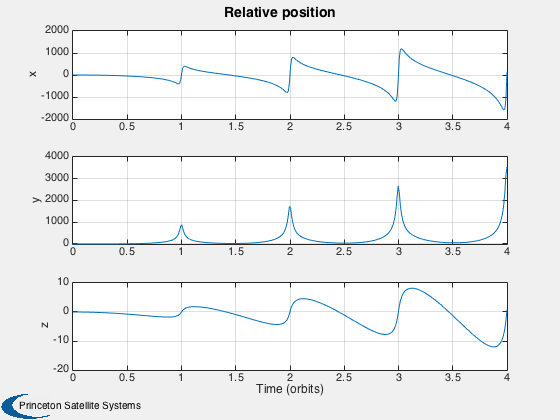
d.el0       = el0;
d.dEl0      = dEl0;
d.t         = t;
d.jD        = jD;
d.unitSun   = unitSun;
d.accSP     = accSP;
d.accSPHills = accSPHills;
d.dEl       = dEl;
d.xH        = xH;
d.xF        = xF;
d.meanAnom  = M;
d.trueAnom  = M;

Plot2D(d.t/T,d.accSPHills,'Time (orbits)',{'x','y','z'},'Solar Accel. in Hills Frame')
Plot2D(d.t/T,d.xH(1:3,:),'Time (orbits)',{'x','y','z'},'Relative position')

%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b