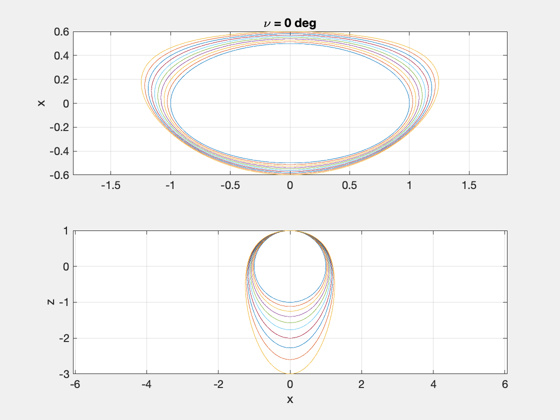
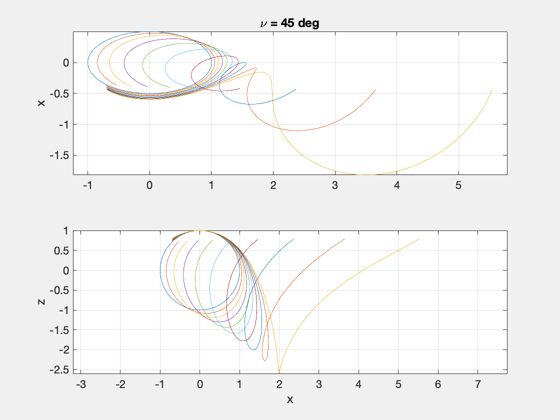
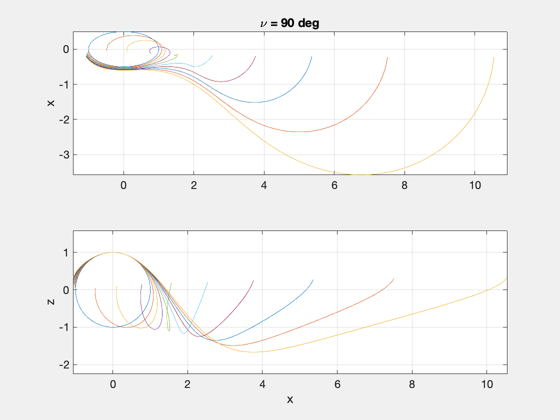
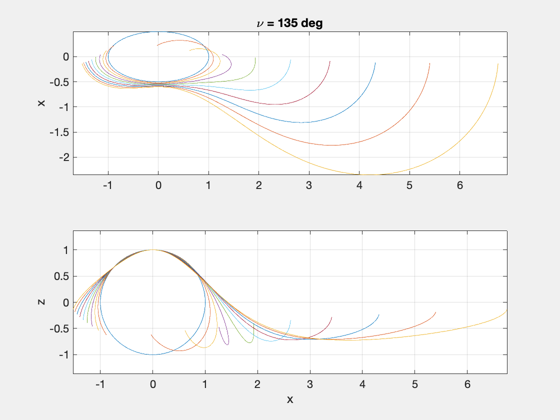
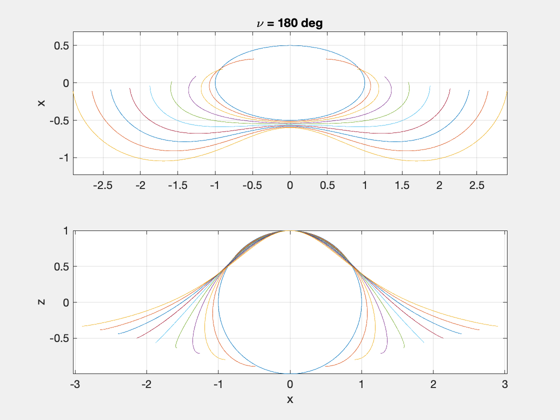
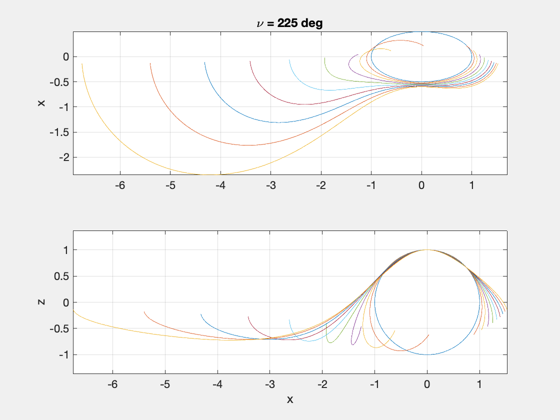
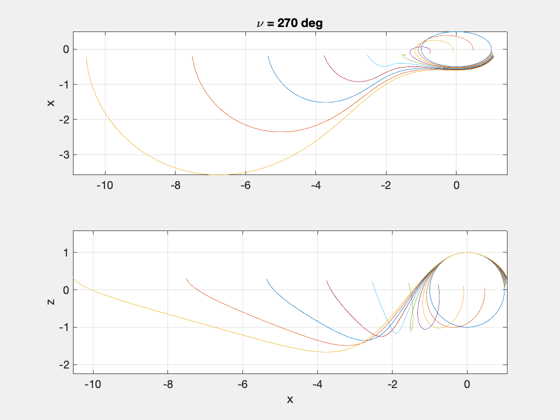
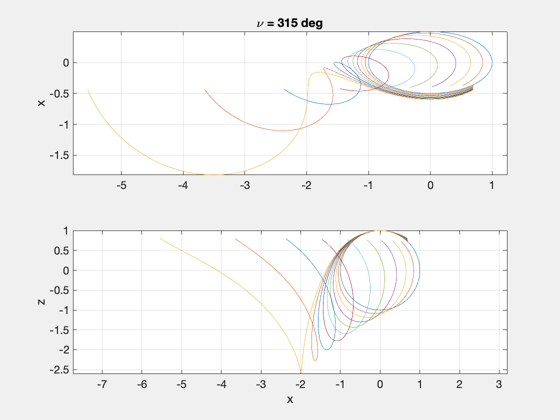
Demonstrate how relative motion changes when the same relative state is initialized at different true anomalies.

Since version 7.
-------------------------------------------------------------------------
References: Inalhan, Tillerson, How, "Relative Dynamics and Control of
Spacecraft Formations in Eccentric Orbits", Journal of Guidance,
Control & Dynamics, Vol.25, No.1, Jan-Feb 2002.%
-------------------------------------------------------------------------
See also FFEccLawdensEqns
-------------------------------------------------------------------------

%--------------------------------------------------------------------------
%	Copyright 2004 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------


nu = 0:pi/180:2*pi;
nP = length(nu);

e  = linspace(.00001,.5,10);

z0  = 1;
dy0 = 1;
xH0 = [0;0;z0;0;dy0;0];

nu0 = [0:45:315]*pi/180;

nE = length(e);
nP = length(nu);

for th0 = nu0

  x = zeros(nE,nP);
  y = zeros(nE,nP);
  z = zeros(nE,nP);

  for i=1:nE,
    xH0(1) = -xH0(5)*(1+e(i))/(2+e(i));
    xH     = FFEccLawdensEqns(xH0,th0,nu,e(i));
    x(i,:) = xH(1,:);
    y(i,:) = xH(2,:);
    z(i,:) = xH(3,:);
  end

  NewFig('FFEccInitDemo');
  subplot(211)
  plot(y',x'); ylabel('x'); grid on, axis equal, zoom on
  title(['\nu = ',num2str(round(th0*180/pi)),' deg']);
  subplot(212)
  plot(y',z'); ylabel('z'); xlabel('x'); grid on, axis equal, zoom on


end



%--------------------------------------
% PSS internal file version information
%--------------------------------------