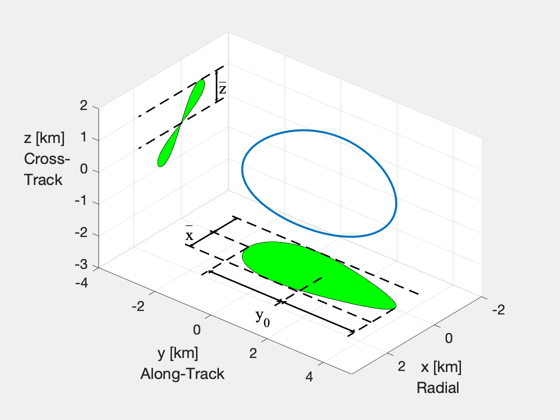
Visualization of eccentric relative orbits

Illustrate the geometric parameters that define a naturally repeating relative trajectory in an eccentric reference orbit.

Since version 7.
------------------------------------------------------------------------------

Parameters
Trajectory
Second example

%-------------------------------------------------------------------------------
%   Copyright (c) 2004 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Parameters

% linewidth for graphics
%-----------------------
lw = 1.5;

% eccentric geometry
%-------------------
e = 0.7;
N = 300;

Trajectory

g = struct('y0',1, 'xMax',1, 'nu_xMax',pi/2, 'zMax',1, 'nu_zMax',pi);
D = FFEccGoals( e, g );
nu = linspace(0,2*pi,N);
xH = FFEccProp( D, nu, e );
figure('position',[0   338   560   420])
plot3( xH(1,:), xH(2,:), xH(3,:), 'linewidth',2 ), hold on, axis equal, grid on
zb = floor(min(xH(3,:))-1)*ones(1,N);
yb = floor(min(xH(2,:))-1)*ones(1,N);
patch( xH(1,:), xH(2,:), zb, 'g' )
patch( xH(1,:), yb, xH(3,:), 'g' )
set(gca,'fontsize',14)
xlabel(' x [km]\newlineRadial',        'units','normalized','position',[.89, .10, 0])
ylabel('    y [km]\newlineAlong-Track','units','normalized','position',[.22, .06, 0])
zlabel('z [km]\newlineCross-\newlineTrack','rotation',0,'horizontalalignment','right')
axis equal, axis([-2 3 yb(1) 3 zb(1) 2])
view([130,30]), cameratoolbar('setmode','orbit')

% z lines
ymin = min(xH(2,:));
ymax = max(xH(2,:));
plot3([-1.8,1.8],[yb(1),yb(1)],[0,0],'k--','linewidth',lw)
plot3([-1.8,1.8],[yb(1),yb(1)],[1,1],'k--','linewidth',lw)

% y lines
plot3([0,2],[ymin,ymin],zb(1:2),'k--','linewidth',lw)
plot3([0,2],[g.y0,g.y0],zb(1:2),'k--','linewidth',lw)
plot3([0,2],[ymax,ymax],zb(1:2),'k--','linewidth',lw)

% x lines
plot3(-[g.xMax,g.xMax],[ymax,ymin-1],zb(1:2),'k--','linewidth',lw)
plot3([g.xMax,g.xMax],[ymax,ymin-1],zb(1:2),'k--','linewidth',lw)
plot3([0,0],[ymin,ymin-1],zb(1:2),'k--','linewidth',lw)

% z arrow and label
zt=text(-1.6,yb(1),.4,'z'); bt=text(-1.6,yb(1),.7,'_');
set(bt,'interpreter','none','fontsize',14);
set(zt,'fontname','times','fontsize',16)
line([-1.5,-1.5],[yb(1),yb(1)],[0,g.zMax],'color','k','linewidth',1.5)
patch([-1.45 -1.55 -1.5],yb(1:3),[.9 .9 1],'k');
patch([-1.45 -1.55 -1.5],yb(1:3),[.1 .1 0],'k');

% y arrows and label
yt=text(2.5,g.y0,zb(1),'y_0');
set(yt,'fontname','times','fontsize',16)
line([1.7 1.7],[ymin,ymax],[zb(1),zb(1)],'color','k','linewidth',1.5)
patch([1.8, 1.6, 1.7],[.1, .1, 0]+ymin,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[.1, .1, 0]+g.y0,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[-.1, -.1, 0]+g.y0,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[-.1, -.1, 0]+ymax,zb(1)+[0 0 0],'k')

% x arrow and label
xt=text(g.xMax*.6,ymin-1.25,zb(1),'x'); bt=text(g.xMax*.6,ymin-1.25,zb(1)+.35,'_');
set(bt,'interpreter','none','fontsize',14);
set(xt,'fontname','times','fontsize',16)
line([0,g.xMax],[ymin,ymin]-.75,zb(1:2),'color','k','linewidth',1.5)
patch([.1 .1 0],ymin-.75+[-.05 .05 0],zb(1:3),'k');
patch(g.xMax-[.1 .1 0],ymin-.75+[-.05 .05 0],zb(1:3),'k');
line([0,-g.xMax],[ymin,ymin]-.75,zb(1:2),'color','k','linewidth',1.5)
patch(-[.1 .1 0],ymin-.75+[-.05 .05 0],zb(1:3),'k');
patch(-g.xMax+[.1 .1 0],ymin-.75+[-.05 .05 0],zb(1:3),'k');

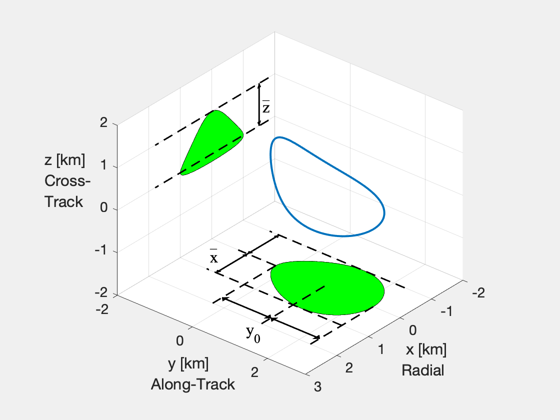
Second example

e = 0.6;
g = struct('y0',1, 'xMax',1, 'nu_xMax',-pi/2, 'zMax',1, 'nu_zMax',E2Nu(e,pi/2) );
D = FFEccGoals( e, g );
nu = linspace(0,2*pi,N);
xH = FFEccProp( D, nu, e );
figure('position',[560   338   560   420])
plot3( xH(1,:), xH(2,:), xH(3,:), 'linewidth',2 ), hold on, axis equal, grid on
zb = floor(min(xH(3,:))-1)*ones(1,N)-1;
yb = floor(min(xH(2,:))-1)*ones(1,N)-1;
patch( xH(1,:), xH(2,:), zb, 'g' )
patch( xH(1,1:N/2), yb(1:N/2), xH(3,1:N/2), 'g' )
patch( xH(1,N/2+1:end), yb(N/2+1:end), xH(3,N/2+1:end), 'g' )
set(gca,'fontsize',14)
xlabel(' x [km]\newlineRadial',        'units','normalized','position',[.89, .05, 0])
ylabel('    y [km]\newlineAlong-Track','units','normalized','position',[.22, .09, 0])
zlabel('z [km]\newlineCross-\newlineTrack','rotation',0,'horizontalalignment','right')
axis equal, axis([-2 3.5 yb(1) 5 zb(1) 2])
view([130,30]), cameratoolbar('setmode','orbit')

% z lines
plot3([-1.8,1.8],[yb(1),yb(1)],[0,0],'k--','linewidth',lw)
plot3([-1.8,1.8],[yb(1),yb(1)],[1,1],'k--','linewidth',lw)

% y lines
ymin = min(xH(2,:));
ymax = max(xH(2,:));
plot3([0,2],[ymin,ymin],zb(1:2),'k--','linewidth',lw)
plot3([0,2],[g.y0,g.y0],zb(1:2),'k--','linewidth',lw)
plot3([0,2],[ymax,ymax],zb(1:2),'k--','linewidth',lw)

% x lines
plot3(-[g.xMax,g.xMax],[ymax,ymin-1.5],zb(1:2),'k--','linewidth',lw)
plot3( [g.xMax,g.xMax],[ymax,ymin-1.5],zb(1:2),'k--','linewidth',lw)
plot3( [     0,     0],[ymin,ymin-1.5],zb(1:2),'k--','linewidth',lw)

% z arrow and label
zt=text(-1.6,yb(1),.4,'z'); bt=text(-1.6,yb(1),.8,'_');
set(bt,'interpreter','none','fontsize',14);
set(zt,'fontname','times','fontsize',16)
line([-1.5,-1.5],[yb(1),yb(1)],[0,g.zMax],'color','k','linewidth',1.5)
patch([-1.45 -1.55 -1.5],yb(1:3),[.9 .9 1],'k');
patch([-1.45 -1.55 -1.5],yb(1:3),[.1 .1 0],'k');

% y arrows and label
yt=text(2.8,g.y0,zb(1),'y_0');
set(yt,'fontname','times','fontsize',16)
line([1.7 1.7],[ymin,ymax],[zb(1),zb(1)],'color','k','linewidth',1.5)
patch([1.8, 1.6, 1.7],[.1, .1, 0]+ymin,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[.1, .1, 0]+g.y0,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[-.1, -.1, 0]+g.y0,zb(1)+[0 0 0],'k')
patch([1.8, 1.6, 1.7],[-.1, -.1, 0]+ymax,zb(1)+[0 0 0],'k')

% x arrow and label
xt=text(g.xMax*.6,ymin-1.75,zb(1),'x'); bt=text(g.xMax*.6,ymin-1.75,zb(1)+.5,'_');
set(bt,'interpreter','none','fontsize',14);
set(xt,'fontname','times','fontsize',16)
line([0,g.xMax],[ymin,ymin]-1.25,zb(1:2),'color','k','linewidth',1.5)
patch([.1 .1 0],ymin-1.25+[-.05 .05 0],zb(1:3),'k');
patch(g.xMax-[.1 .1 0],ymin-1.25+[-.05 .05 0],zb(1:3),'k');
line([0,-g.xMax],[ymin,ymin]-1.25,zb(1:2),'color','k','linewidth',1.5)
patch(-[.1 .1 0],ymin-1.25+[-.05 .05 0],zb(1:3),'k');
patch(-g.xMax+[.1 .1 0],ymin-1.25+[-.05 .05 0],zb(1:3),'k');

%  ------------------------------------
% PSS internal file version information
%  ------------------------------------

Visualization of eccentric relative orbits

Contents

Parameters

Trajectory

Second example