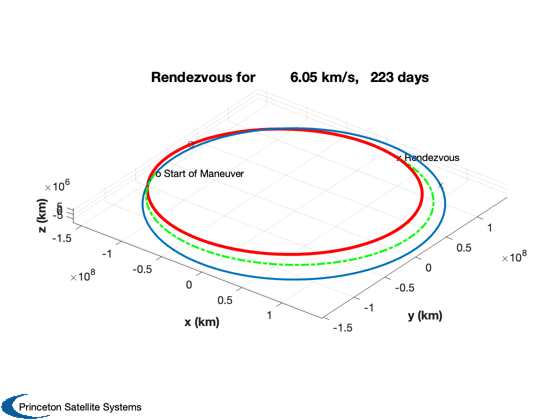
Apophis 3D Lambert transfer delta-V analysis

Starts with plotting the Earth and Apophis orbits. It thens uses PlanetTransferLambert to find the minimum delta-V for impulsive burns. This can be used to help design the low-thrust trajectory. The low-thrust problem is a rendezvous problem.

See PorkChopTOFKepler to generate pork chop plots for Earth/Apophis missions.

See also: Constant, ApophisOrbit, Date2JD, AdjustMeanAnomaly, RVOrbGen, PlanetPosJPL, NewFig, JD2Date, PlanetTransferLambert, Mag, Plot2D, AddFillToPlots, Figui

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2023.1 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2023.1
%--------------------------------------------------------------------------

Constants

dayToSec      = 86400;
mu            = Constant('mu sun');

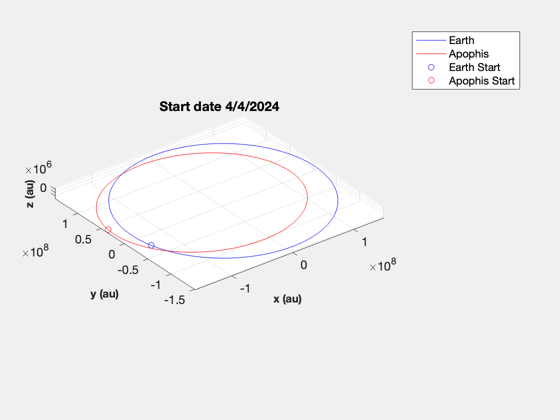
Generate the Earth and Apophis orbit

Generate Apophis orbit from Keplerian elements and the Earth ephemeris from PlanetPosJPL with 405 ephemeris data.

[elA,~,~,jDA] = ApophisOrbit;
jD0           = Date2JD([2024 4 4]);
el            = AdjustMeanAnomaly(elA,jDA,jD0);
nDays         = 366;
t             = 0:nDays;
jD            = jD0 + t;
[rApophis,vApophis] = RVOrbGen(elA,t*86400,[],mu);

PlanetPosJPL( 'initialize', 3 );

rEarth = zeros(3,length(jD));
vEarth = zeros(3,length(jD));

for k = 1:length(jD)
  [rEarth(:,k),~,vEarth(:,k)] = PlanetPosJPL( 'update', jD(k), 1 );
end

NewFig('Apophis and Earth')
plot3(rEarth(1,:),rEarth(2,:),rEarth(3,:),'b');
hold on
plot3(rApophis(1,:),rApophis(2,:),rApophis(3,:),'r');
XLabelS('x (au)');
YLabelS('y (au)');
ZLabelS('z (au)');
axis image
grid on
rotate3d on
plot3(rEarth(1,1),rEarth(2,1),rEarth(3,1),'ob');
hold on
dS = JD2Date(jD0);
title(sprintf('Start date %d/%d/%d',dS(2),dS(3),dS(1)));
plot3(rApophis(1,1),rApophis(2,1),rApophis(3,1),'or');
legend('Earth','Apophis','Earth Start', 'Apophis Start')

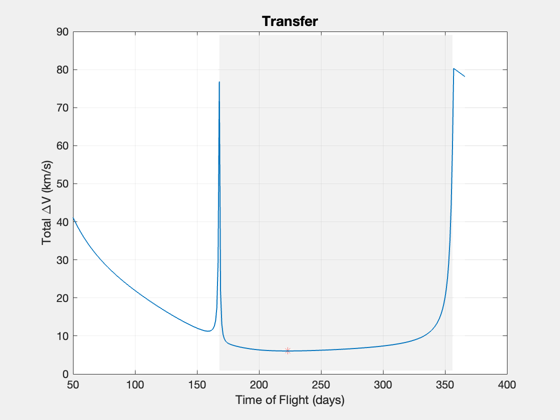
Use PlanetTransferLambert to find the needed impulsive burns

tOF = 50:nDays;
dV  = zeros(1,length(tOF));
tM  = zeros(1,length(tOF));

for k = 1:length(tOF)
  [dV(k),~,~,~,tM(k)] = PlanetTransferLambert( jD0, tOF(k)*dayToSec, 'earth', elA );
end

[~,kk] = min(dV);
PlanetTransferLambert( jD0, tOF(kk)*dayToSec, 'earth', elA )

Plot2D(tOF,dV,'Time of Flight (days)','Total \DeltaV (km/s)','Transfer')
hold on
plot(tOF(kk),dV(kk),'r*')
AddFillToPlots(tOF,tM,gcf)

Figui;


%--------------------------------------

% $Id: eb1b0bb78336eca4c00ea07778e2bcc0cf0123a0 $

Published with MATLAB® R2024a