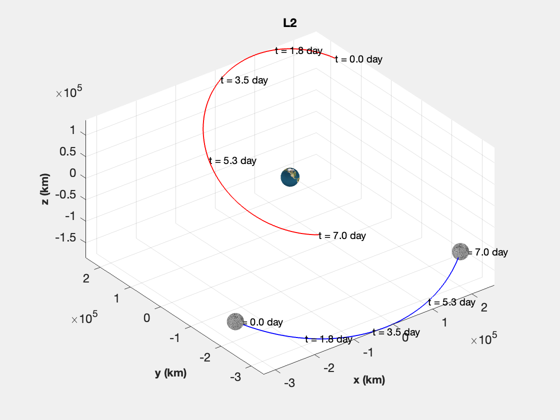
Simulate a spacecraft in orbit near the earth and moon.

Uses two stored gravity files, EarthGravityModel.mat and LunarGravityModel.mat. ------------------------------------------------------------------------ See also FEarthMoonSun, LagrangePointsL1ToL5, and TransformLagrangePoints. , Constant, Plot2D, TimeGUI, TimeLabl, TitleS, Date2JD ------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%  Copyright (c) 2004 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Globals for the GUI

%--------------------
global simulationAction
simulationAction = ' ';

Spacecraft Mass

%----------------
d                 = struct('mass',1000);
d.jDStart         = Date2JD; % Today
d.muSun           = 1.327124e+11;
kLP               = 2;

These have been saved in mat files

%-----------------------------------
d.earth           = load('EarthGravityModel.mat');
d.moon            = load('LunarGravityModel.mat');

Use point mass models

%----------------------
d.earth.nZ        = 0;
d.earth.nT        = 0;
d.moon.nZ         = 0;
d.moon.nT         = 0;

The number of steps

%--------------------
nSim          = 800;

Create the time array

%----------------------
tDuration     = 7*86400;
t             = linspace(0,tDuration,nSim);
dT            = t(2) - t(1);

Specify the ode113 accuracy

%----------------------------
xODEOptions   = odeset( 'AbsTol', 1e-16, 'RelTol', 1e-13 );

Set up the position and velocity vectors. Units are km and km/s.

%-----------------------------------------------------------------
muMoon  = Constant('mu moon');
muEarth = Constant('mu earth');
p       = LagrangePointsL1ToL5( muMoon/muEarth );
TransformLagrangePoints( p, d.jDStart  )
[r, v] = TransformLagrangePoints( p, d.jDStart  );
x      = [r(:,kLP);v(:,kLP)];

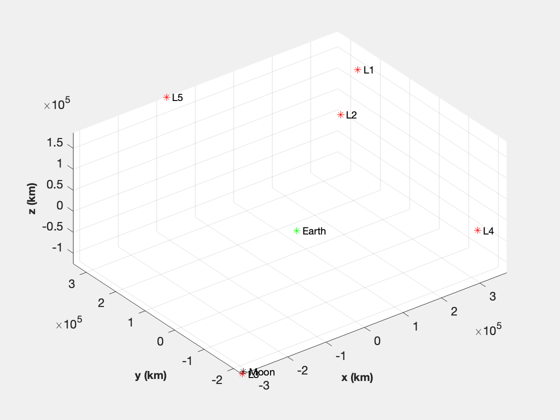
Initialize the time display

%----------------------------
tToGoMem.lastJD        = 0;
tToGoMem.lastStepsDone = 0;
tToGoMem.kAve          = 0;
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, tToGoMem, 0, dT, 'Earth-Moon-Sun Simulation' );

Initialize the plotting array

%------------------------------
xPlot      = zeros(6,nSim);
xPlot(:,1) = x;

Flag

%-----
dontPlot   = 0;

Simulate

%---------
for k = 2:nSim

	% Display the status message
	%---------------------------
	[ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

  % Force
  %------
  d.force       = [0;0;0];

	% Propagator
	%-----------
	[z, x]        = ode113( 'FEarthMoonSun', [t(k-1) t(k)], x, xODEOptions, d );
	x             = x(end,:)';
	xPlot(:,k)    = x;

	% User controls on the GUI
	%-------------------------
	switch simulationAction
    	case 'pause'
        pause
        simulationAction = ' ';
    	case 'stop'
	  		dontPlot = 1;
      	break;
    	case 'plot'
     		break;
	end
end

Close the time GUI

%-------------------
close( tToGoMem.hGUI.fig );

Quit if you hit the stop button

%--------------------------------
if( dontPlot )
  return;
end

Plot the orbit

%---------------
j      = 1:k;
jD     = d.jDStart + t/86400;
[t, c] = TimeLabl( t(j) );
Plot2D( t, xPlot(:,j), c, {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y(km/s)' 'v_z(km/s)'}, 'ECITrajectory' );

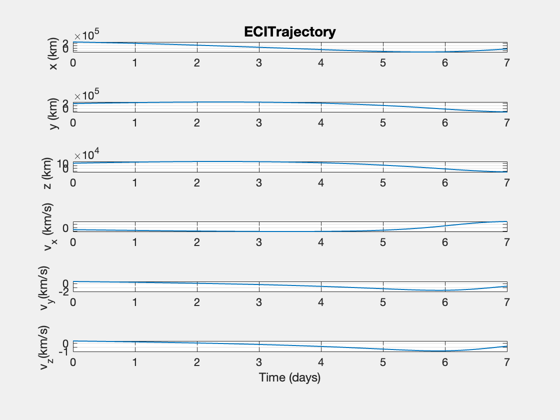
Plot the earth, moon and trajectory in 3D

%------------------------------------------
EarthMoon( xPlot(:,j), jD(j), [3 10] );
TitleS(sprintf('L%i',kLP))


%--------------------------------------
% PSS internal file version information
%--------------------------------------

% $Id: f9bdfd282961623f40a3287a470d2f1e222038dd $

Published with MATLAB® R2024a