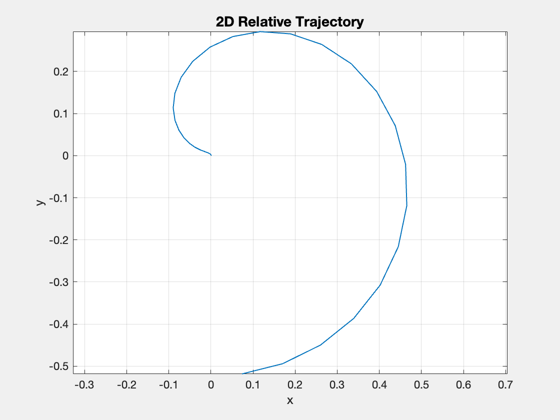
Perform an optimal 2D transfer from Earth to Mars orbits.

This performs a discrete optimization of a linearized system using Simplex. The mass of the spacecraft (and the acceleration) is assumed to be constant.

See also Constant, BarPlot, NewFig, TimeLabl, TitleS, XLabelS, YLabelS, Mag, OptimalTrajectory, LTSpiral, LinOrb, Planets

Specify planets: Earth and Mars
Spacecraft
Low-thrust spiral duration
Linearize the orbit
We only care about the orbit radius, radial velocity and tangential velocity
Display the output

%-------------------------------------------------------------------------------
%   Copyright (c) 2002 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

clear f;

Specify planets: Earth and Mars

p             = Planets( 'rad', [3 4] );
AU            = Constant('au');
muSun         = Constant('mu sun');
aEarth        = AU*p.a(1);
aMars         = AU*p.a(2);

Spacecraft

thrust = 0.04; % N
mass   = 127;  % kg
factor = 2;    % increase the thrust for the optimization if it fails to converge

Low-thrust spiral duration

ex. for 0.4 N and 127 kg, duration is 20.7 days

dVEarthToMars = LTSpiral( p.a(1)*AU, p.a(2)*AU, [], muSun );
% duration is deltaV/acceleration
duration      = dVEarthToMars*1000/(thrust/mass)/86400;
fprintf('\nLow thrust spiral DV:       %g km/s\n',dVEarthToMars);
fprintf('Low thrust spiral duration: %g days\n',duration);

Low thrust spiral DV:       5.65517 km/s
Low thrust spiral duration: 207.814 days

Linearize the orbit

state x: [dr;rtheta;z;ddr/dt;drtheta/dt;dz/dt]

n             = sqrt(muSun/aEarth)/aEarth;
[a, b, c, d]  = LinOrb( [], n, [] );

We only care about the orbit radius, radial velocity and tangential velocity

%-----------------------------------------------------------------------------
f.a    = a([1 4 5],[1 4 5]);
f.b    = b([1 4 5],[1 2]); % inputs are radial and tangential accel

nDays  = ceil(1.05*duration);
nPts   = 30;
dT     = nDays*86400/nPts;
t      = (0:nPts)*dT; % fixed end time

x0     = [0;0;0]; % [dr;ddr/dt;drtheta/dt]

rF     = aMars - aEarth; % the change in radius (km)
yDot   = -3*n*rF/2;      % the final tangential velocity (km/s)
xF     = [rF;0;yDot];

uMax   = factor*thrust/mass*1e-3; % maximum control (km/s^2) [0.0105/127]

% u is the control - the acceleration profile [radial;tangential]
[err, u, x] = OptimalTrajectory( x0, xF, t, uMax, f );

Display the output

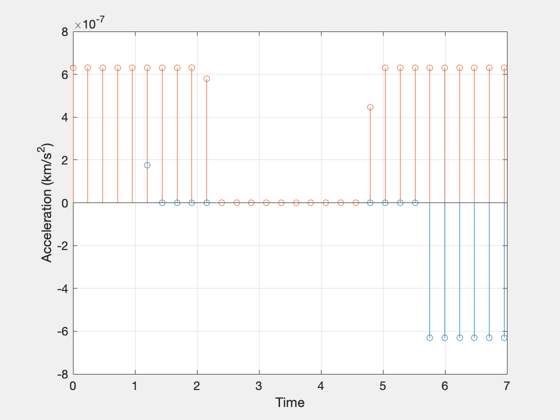
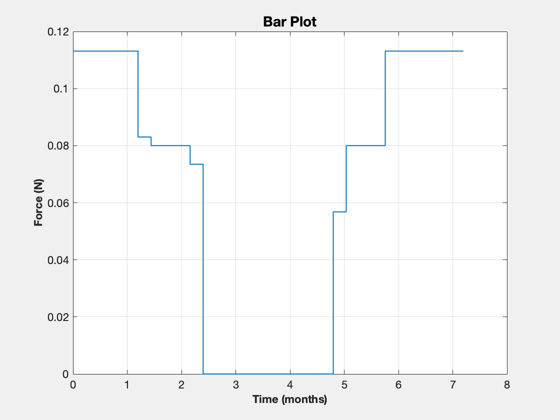
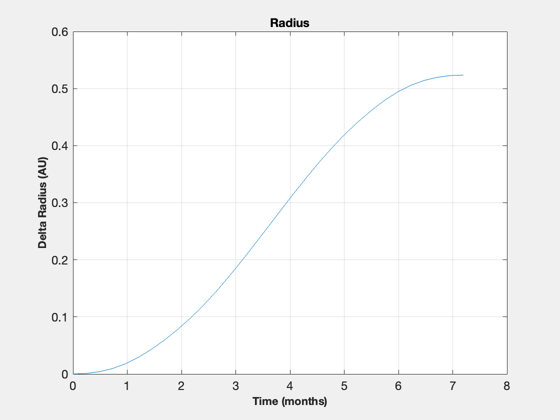
[tP, tL] = TimeLabl( t );

mU = Mag(u);
uF = 1000*mU*mass; % convert to force
dV = sum(mU)*dT;

vOverR = x(3,:)./x(1,:);
vOverR(isnan(vOverR)) = 0;
theta = cumtrapz(vOverR)*dT;
c = cos( theta );
s = sin( theta );
Plot2D( x(1,:).*c/AU, x(1,:).*s/AU, 'x','y','2D Relative Trajectory')
axis equal


fprintf('\nOptimal 2D DV: %g km/s\n',dV);

NewFig('Optimal Control')
stem(tP(1:end-1),u')
ylabel('Acceleration (km/s^2)')
xlabel('Time')
grid on

BarPlot(tP, uF )
XLabelS(tL);
YLabelS('Force (N)');

NewFig('Radius')
plot( tP, x(1,:)/AU);
XLabelS(tL);
YLabelS('Delta Radius (AU)');
grid on
TitleS('Radius')


%--------------------------------------
% PSS internal file version information
%--------------------------------------

% $Id: e9505b3489202a0c275489a6fe04d2070ca1769b $

Optimal 2D DV: 9.6239 km/s