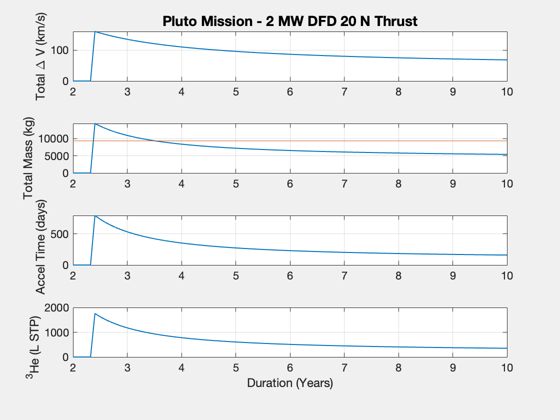
Pluto mission delta-Vs using DFD, Lambert solutions

Use Lambert to calculate the delta-V to Pluto over a range of transit times, from 2 to 10 years. Estimate the total mission mass using specific power to scale the spacecraft, plus allowing for a given tank fraction, thrust efficiency, and a payload of 1000 kg. Creates PlutoSpacecraftData.mat which is used by the CAD model for sizing the fuel and power systems.

See also Constant, SaveStructure, Plot2D, Plot3D, Date2JD, RK4, Mag, LambertTOF, VEscape, RocketMass, FOrbCart, RV2El, PlanetPosition

Script parameters
Lambert analysis
Plot the mission

%--------------------------------------------------------------------------
%   Copyright (c) 2015 Princeton Satellite Systems, Inc.
%   All Rights Reserved.
%--------------------------------------------------------------------------
%   Since version 2016.1
%--------------------------------------------------------------------------

Script parameters

These are the parameters that define the mission analysis. For simplicity we must assume a fixed thrust and Isp throughout the mission. The engine mass will be calculated solely based on the specific power.

% Payload mass (kg)
mPLD      = 1000;
% Assume a specific power
kWPerKg   = 1.2;
% Total engine power
power     = 2e6; % W
% Tank structural fraction
tankF     = 0.02;
% Engine thrust
thrust    = 20;  % N
% Engine efficiency
eff       = 0.5;

% orbital altitude at Pluto (km)
h         = 600;
% Epoch
jD0        = Date2JD([2028 7 2 0 0 0]);

% Fusion fuel computations
He3_STP = 0.1339;
rho3He = 59;                % density of liquid 3He, kg/m3
amu3He = 1.6605e-27*3.016;  % mass of 3He atom, kg
ePerReaction = 18.3;        % MeV, energy per D-3He reaction
eJPerReaction = ePerReaction*1e6*1.602e-19; % J per reaction

Lambert analysis

Perform an analysis of the transfer to Pluto for an array of mission durations.

% Constants
muSun     = Constant('mu sun');
muPluto   = Constant('mu pluto');
rPluto    = Constant('equatorial radius pluto');
aU        = Constant('au');

% Mass of the engine, using specific power
massDFD   = power/kWPerKg/1000;

% Exhaust velocity - will be fixed
uE        = 2*power*eff/thrust;

PlanetPosition( 'initialize', [3 9] );
[r0, ~, v]  = PlanetPosition( 'update', jD0 );
dVOrbit     = VEscape(rPluto+h,muPluto) - sqrt(muPluto/(rPluto+h));

years       = linspace(2,10);
n           = length(years);
dV          = zeros(1,n);
mF          = zeros(1,n);
mT          = zeros(1,n);
tAccel      = zeros(1,n);
hE3         = zeros(1,n);
for k = 1:n
  duration      = years(k)*365.25;
  [rI, ~, vI]   = PlanetPosition( 'update', jD0+duration );
  vT            = LambertTOF( r0(:,1), rI(:,2), duration*86400, 1, muSun );

  dV(k)         = Mag(vT(:,1) - v(:,1)) + Mag(vT(:,2) - vI(:,2));

  dVTotal       = dV(k) + dVOrbit;
  [mF(k),mT(k)] = RocketMass( uE/9.806, mPLD+massDFD, tankF, dVTotal );
  accel         = thrust/(mT(k) - 0.5*mF(k));
  tAccel(k)     = dV(k)*1000/accel/86400;

  % if available, see He3MassFromPower
  if exist('He3MassFromPower','file')
    [~,~,vol]   = He3MassFromPower( power*tAccel(k)*86400 );
    hE3(k)      = vol(1);
  else
    energy      = power*tAccel(k)*86400;
    mass3He     = amu3He*energy/eJPerReaction;
    hE3(k)      = mass3He*1e3/He3_STP;
  end

  if tAccel(k)>duration
    tAccel(k) = 0;
    dV(k) = 0;
    mF(k) = 0;
    mT(k) = 0;
    hE3(k) = 0;
  end
end

yL = {'Total \Delta V (km/s)' 'Total Mass (kg)' 'Accel Time (days)' '^3He (L STP)'};
titleStr = sprintf('Pluto Mission - %d MW DFD %d N Thrust',round(power/1e6),round(thrust));
Plot2D(years,[dV;mT;tAccel;hE3],'Duration (Years)', yL,titleStr)
subplot(4,1,2)
hold on
yy = axis;
plot(yy(1:2),9306*[1 1])

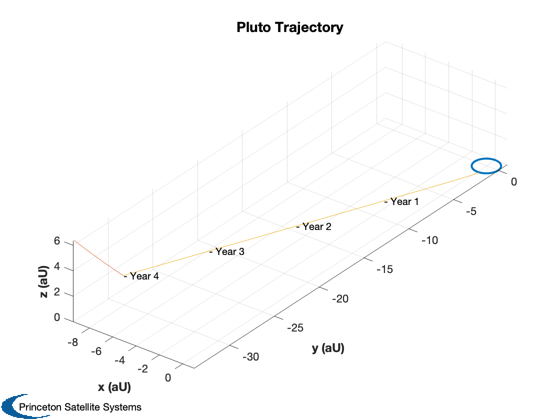
Plot the mission

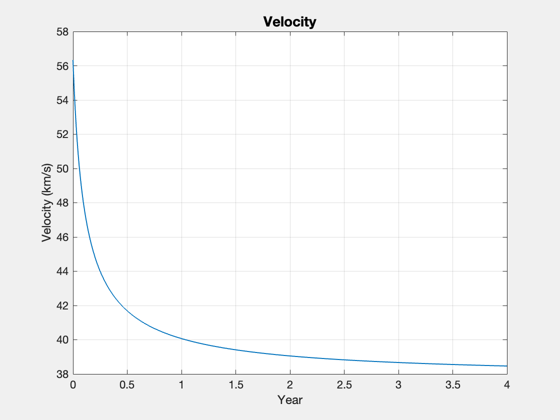
yearsMission  = 4; % selected from prior plot
duration      = yearsMission*365.25;
[rI, ~, vI]   = PlanetPosition( 'update', jD0+duration );
[vT, a]       = LambertTOF( r0(:,1), rI(:,2), duration*86400, 1, muSun );
dV            = Mag(vT(:,1) - v(:,1)) + Mag(vT(:,2) - vI(:,2));
dVTotal       = dV + dVOrbit;

[massFuelPluto, massTotalPluto] = RocketMass( uE/9.806, mPLD+massDFD, tankF, dVTotal );

accel         = thrust/(massTotalPluto - 0.5*massFuelPluto);

% Calculate the 3He mass for the mission. See also He3MassFromPower in the
% FusionPropulsion module, if available.
tAccel        = dV*1000/accel/86400;
energy3He     = 18.3*1.6e-19*1e6;   % J per D-3He reaction
energyTotal   = power*tAccel*86400; % accel time only
mHe3          = 5.0082e-27; % kg
massHe3       = mHe3*energyTotal/energy3He;

% Perform a point-mass heliocentric simulation
n             = 1000;
rE            = zeros(3,n);
rP            = zeros(3,n);
vM            = zeros(1,n);
day           = jD0 + linspace(0,duration,n);
x             = [r0(:,1);vT(:,1)]; % Note the 25% increase in velocity
rT            = zeros(3,n);
el            = RV2El(x(1:3),x(4:6),muSun);
dT            = (day(2)-day(1))*86400; % sec

for k = 1:n
  r       = PlanetPosition('update',day(k));
  rE(:,k) = r(:,1);
  rP(:,k) = r(:,2);
  rT(:,k) = x(1:3);
  vM(1,k) = Mag(x(4:6));
  x       = RK4(@FOrbCart,x,dT,0,[0;0;0],muSun);
end

% Plot the trajectory with the planet orbits
rE = rE/aU;
rP = rP/aU;
rT = rT/aU;
Plot3D( rE, 'x (aU)', 'y (aU)', 'z (aU)', 'Pluto Trajectory' )
hold on
plot3(rP(1,:),rP(2,:),rP(3,:));
plot3(rT(1,:),rT(2,:),rT(3,:));
% Add year labels
year = (day - jD0)/365.25;
j    = ceil(linspace(1,n,5));
for k = 2:5
  i = j(k);
  text(rT(1,i), rT(2,i), rT(3,i),sprintf('- Year %d',floor(year(i))));
end

% Plot the velocity magnitude
Plot2D(year,vM,'Year','Velocity (km/s)','Velocity')

% Store mission data
q           = struct;
q.massHe3   = massHe3;
q.massFuel  = massFuelPluto;
q.massDFD   = massDFD;
q.massPld   = mPLD;
q.power     = power;
q.specPower = kWPerKg;
thisP       = fileparts(mfilename('fullpath'));
SaveStructure(q,fullfile(thisP,'PlutoSpacecraftData'));


%--------------------------------------

% $Id: 5ea6683046bbd766bc08cabbb746138a730b93d8 $

Pluto mission delta-Vs using DFD, Lambert solutions

Contents

Script parameters

Lambert analysis

Plot the mission