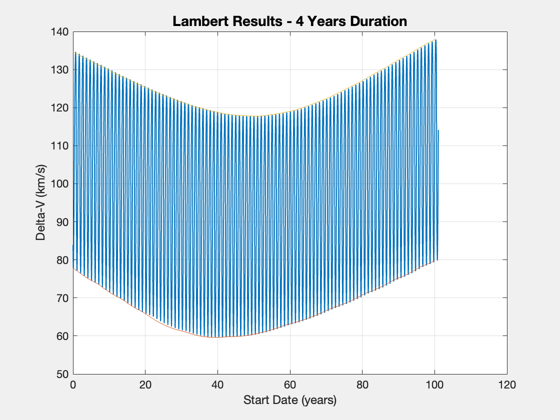
Lambert Delta-V to Pluto for fixed duration and variable start date

Perform a Lambert analysis for a fixed time of flight and an array of start dates, considering the true planetary positions (from the almanac). Calculate the minimum delta-V vs. start date in years from Jan, 1, 2016. Will create a plot of the delta-V envelope per start date for the chosen duration.

% See also: PlanetPosition, LambertTOF, Mag

%---------------------------------------------------------------------
%   Copyright (c) 2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%---------------------------------------------------------------------

% Constants
muSun     = Constant('mu sun');
muPluto   = Constant('mu pluto');
rPluto    = Constant('equatorial radius pluto');
g         = 9.806;

% Epoch
jD0         = Date2JD([2016 1 1 0 0 0]);
PlanetPosition( 'initialize', [3 9] );

% Vary the start date over 100 years but use a fixed time of flight
h         = 600; % orbital altitude at Pluto (km)
dVOrbit   = sqrt(muPluto/(rPluto+h));
nYears    = 4;
nA        = 100;
nPP       = 25;
start     = linspace(0,nA);
nS        = length(start);
duration  = nYears*365.25; % days
dVs       = zeros(1,nS*nPP);
dVMax     = zeros(1,nS);
dVMin     = zeros(1,nS);
p         = 1;
time      = zeros(1,nS*nPP);
for j = 1:nS
  dVThis = zeros(1,nPP);
  for k = 1:nPP
    days = (k-1)*365/nPP;
    time(p)       = start(j)*365.25+days;
	  jDS           = jD0+start(j)*365.25+days;
	  [r0, ~, v]    = PlanetPosition( 'update', jDS );
    [rI, ~, vI]   = PlanetPosition( 'update', jDS+duration );
  % short or long way - doesn't affect minimum, only max
%   Tran = Cross(r0(:,1),rI(:,2));
%   hC   = Cross(rI(:,2),vI(:,2));
%   tM   = sign(hC'*Tran)
    [vT, a]       = LambertTOF( r0(:,1), rI(:,2), duration*86400, 1, muSun );
    dV            = Mag(vT(:,1) - v(:,1)) + Mag(vT(:,2) - vI(:,2));
    dVs(p)        = dV + dVOrbit;
    dVThis(k)     = dVs(p);
    p = p+1;
  end
  dVMin(j) = min(dVThis);
  dVMax(j) = max(dVThis);
end
Plot2D(time/365,dVs,'Start Date (years)','Delta-V (km/s)',sprintf('Lambert Results - %d Years Duration',nYears))
hold on
plot(start,dVMin)
plot(start,dVMax)



%--------------------------------------

% $Id: 9cc8cceea910179c6752a696a32bfade1d31b4eb $

Published with MATLAB® R2024a