GravityTurnDemo

Gravity turn trajectories.
Specify the model
First, replicate the plot in the reference
Plotting
Sensitivity analysis
Optimization

Gravity turn trajectories.

Perform multiple gravity-turn trajectories for the classic Von Braun shuttle design in the reference. As prescribed, the specified "kick angles" differ by less than one degree. Then, we perform a sensitivity analysis for a range of pitchover angles and plot the ratio of the final velocity to orbital velocity. Finally, an optimization is performed with fzero to find the pitchover angle which will result in a zero flight path angle at burnout (horizontal flight).

%--------------------------------------------------------------------------
%	Reference:	Wiesel, W. E., Spaceflight Dynamics, McGraw-Hill, 1988,
%             pp. 207-211 and table 7-2.
%
% See also: LaunchRHSData, MSThrustModel, GravityTurnSim2D, FGravityTurn
%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%    Copyright (c) 2014 Princeton Satellite Systems, Inc.
%    All Rights Reserved.
%--------------------------------------------------------------------------

Specify the model

rocket         = VonBraunRocket;
d              = LaunchRHSData( 2, rocket );
d.cDA          = 0.35*[30 20 10]; % Drag coefficient of each stage times area
d.fThrust      = @MSThrustModel;
pitchover      = [19 19.45 20.4]; % degrees
tPitch         = 10;   % sec

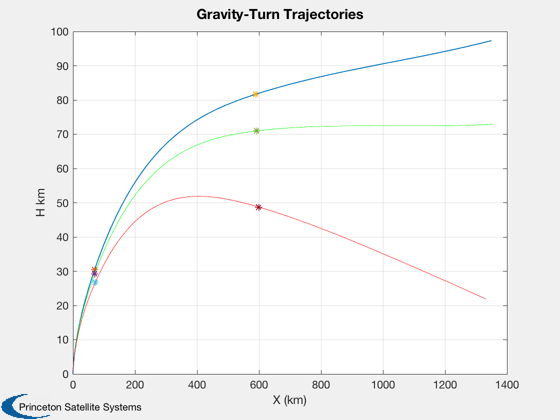
First, replicate the plot in the reference

traj = cell(1,length(pitchover));
for k = 1:length(pitchover)
  disp(' ')
  traj{k} = GravityTurnSim2D( d, pitchover(k), tPitch );
  fprintf('\tFinal velocity: %f\n',traj{k}.x(3,end));
  fprintf('\tOrbital velocity: %f\n',VOrbit(d.Rp+traj{k}.x(2,end)));
end

 
	Pitch-over altitude: 0.419161 km
	Pitch-over velocity: 0.095632 km/s
	Final velocity: 8.880810
	Orbital velocity: 7.845701
 
	Pitch-over altitude: 0.419161 km
	Pitch-over velocity: 0.095632 km/s
	Final velocity: 8.897186
	Orbital velocity: 7.860522
 
	Pitch-over altitude: 0.419161 km
	Pitch-over velocity: 0.095632 km/s
	Final velocity: 7.101403
	Orbital velocity: 7.891829

Plotting

xPlot = traj{1}.x;
Plot2D(xPlot(1,:),xPlot(2,:),'X (km)','H km','Gravity-Turn Trajectories');
hold on

kFirst = find(diff(xPlot(6,:)),1,'first');
kSecnd = find(diff(xPlot(6,:)),1,'last');
plot(xPlot(1,kFirst),xPlot(2,kFirst),'*')
plot(xPlot(1,kSecnd),xPlot(2,kSecnd),'*')

xPlot = traj{2}.x;
plot(xPlot(1,:),xPlot(2,:),'g')

kFirst = find(diff(xPlot(6,:)),1,'first');
kSecnd = find(diff(xPlot(6,:)),1,'last');
plot(xPlot(1,kFirst),xPlot(2,kFirst),'*')
plot(xPlot(1,kSecnd),xPlot(2,kSecnd),'*')

xPlot = traj{3}.x;
plot(xPlot(1,:),xPlot(2,:),'r')

kFirst = find(diff(xPlot(6,:)),1,'first');
kSecnd = find(diff(xPlot(6,:)),1,'last');
plot(xPlot(1,kFirst),xPlot(2,kFirst),'*')
plot(xPlot(1,kSecnd),xPlot(2,kSecnd),'*')

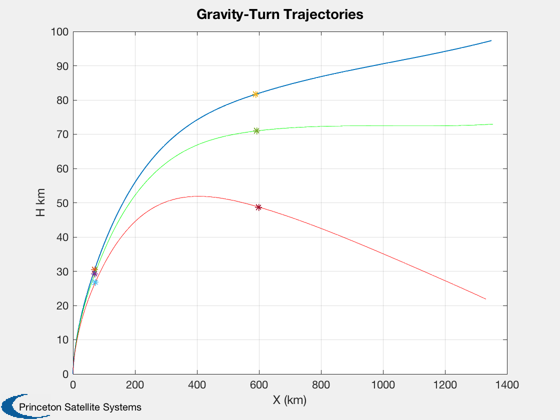
Sensitivity analysis

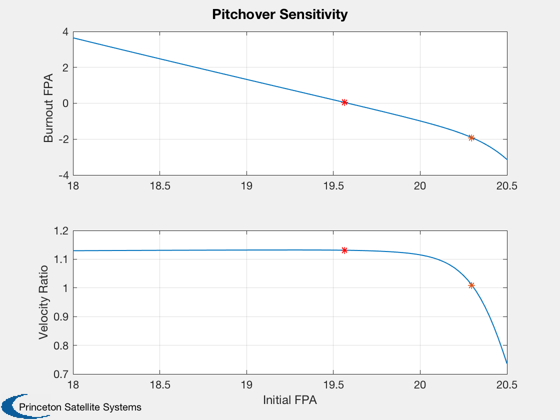
Next, look at the sensitivity for a larger array of initial pitchover angles. The ratio of the final velocity to orbital velocity is plotted.

disp('Evaluate 100 pitch angles...')
angles = linspace(18,20.5,100);
fpa = zeros(1,100);
vel = zeros(1,100);
for k = 1:100
  traj = GravityTurnSim2D( d, angles(k), tPitch, false );
  fpa(k) = traj.x(4,end);
  vel(k) = traj.x(3,end)/VOrbit(traj.x(2,end)+d.Rp);
end
Plot2D(angles,[fpa*180/pi;vel],'Initial FPA',{'Burnout FPA','Velocity Ratio'},'Pitchover Sensitivity');
kVel = find(vel>1,1,'last');
kFPA = find(fpa>0,1,'last');
subplot(2,1,2)
hold on
plot(angles(kVel),vel(kVel),'*')
plot(angles(kFPA),vel(kFPA),'r*')
subplot(2,1,1)
hold on
plot(angles(kVel),fpa(kVel)*180/pi,'*')
plot(angles(kFPA),fpa(kFPA)*180/pi,'r*')

Evaluate 100 pitch angles...

Optimization

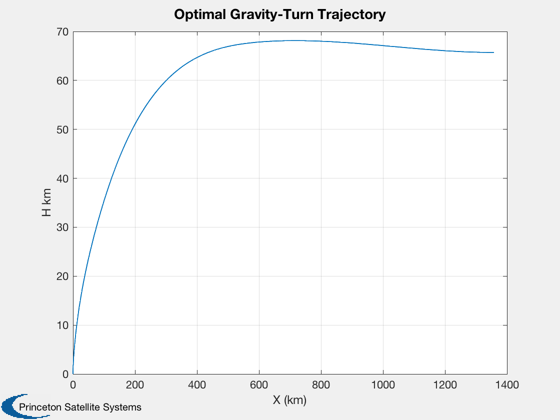
Finally, perform an optimization for the target pitchover angle

fpaOpt = fzero(@(x) FGravityTurn(x,d,tPitch),19);
traj = GravityTurnSim2D( d, fpaOpt, tPitch );
Plot2D(traj.x(1,:),traj.x(2,:),'X (km)','H km','Optimal Gravity-Turn Trajectory');
fprintf(1,'\n\tPitchover with zero burnout FPA: %f\n',fpaOpt);
fprintf(1,'\tFinal velocity: %f\n',traj.x(3,end));
fprintf(1,'\tOrbital velocity: %f\n',VOrbit(d.Rp+traj.x(2,end)));


%--------------------------------------