Solve for the initial conditions to perform a gravity turn trajectory.

Iterate to compute the flight path angle perturbation (pitchover) to
achieve a gravity turn launch trajectory that results in the desired
flight path angle at burnout. Compare this ad hoc approach to the
optimization performed in GravityTurnDemo.
------------------------------------------------------------------------
See also RHSLaunchVehicle2D, MSThrustModel, RK4
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%	Copyright (c) 2007 Princeton Satellite Systems, Inc. All rights reserved
%--------------------------------------------------------------------------

Initialize everything

%----------------------

dT             = 0.5;
mStage         = 5000; % Dry mass of each stage
mFuel          = 100000;
thrust         = 1.7e3; % Thrust of each stage (kN)
Isp            = 405;
lv             = CreateRocketModel(mStage,mFuel,thrust,Isp,'SingleStage','l');
d              = LaunchRHSData(2,lv);
d.aE           = 0;
d.cDA          = 1; % Drag coefficient of each stage times area
gammaP0        = 0.01; % Initial guess for pitchover angle

useRockot = true;
if useRockot
  lv             = RocketDatabase('rockot');
  lv             = SetPayloadMass(lv,1000);
  d.rocket       = lv;
  d.cDA          = 0.35*[5 5 0]; % Drag coefficient of each stage times area
  d.aE           = 0;
  gammaP0        = 0.05; % Initial guess for pitchover angle
end

nSim           = ceil(sum(lv.tBurn)/dT)+1;
gammaFinalDes  = 0; % horizontal flight
gammaFinal     = 1;
kPitch         = 10;
nTry           = 10;
tol            = 1e-8;

gammas = zeros(2,nTry);
j = 1;

Numerical loop around the simulation

format long g
fprintf(1,'\tPitch-over angle \t FPA at burnout\n');
while( j<nTry && abs(gammaFinalDes-gammaFinal)>tol )

   if( j==1 )
      % initial guess
      gammaPitchover = gammaP0;
      gammaPitchoverPrev = 0;
      gammaFinalPrev = gammaFinalDes;
   else
      % Adjust pitchover
      deltaGamma0 = gammaPitchover - gammaPitchoverPrev;
      gammaPitchoverPrev = gammaPitchover;
      gammaPitchover = gammaPitchover - (deltaGamma0/deltaGammaF)*(gammaFinal - gammaFinalDes);
   end

   % Run the sim
   %------------
   x = [0; 0; 0; pi/2; lv.mSP'];  % [range  alt  vel  gamma massFuel]
   xPlot = zeros(length(x),nSim);
   for k = 1:nSim

      xPlot(:,k) = x;

      % Initiate pitchover
      %-------------------
      if( k == kPitch )
         x(4) = pi/2 - gammaPitchover;
      end

      % Propagate one step
      %-------------------
      x = RK4( @RHSLaunchVehicle2D, x, dT, 0, d );

      % stop at burnout
      if( x(end) <= 0 )
         hFinal = x(2);
         vFinal = x(3);
         deltaGammaF = x(4) - gammaFinal;
         gammaFinal = x(4);
         gammas(:,j) = [gammaPitchover;gammaFinal];
         disp(gammas(:,j)')
         break;
      end

   end
   j = j+1;

end
gammas = gammas(:,1:j-1);

	Pitch-over angle 	 FPA at burnout
                      0.05         0.188723106468457
        0.0616312388515672          0.13746062320256
        0.0928204680752305       -0.0384572642657701
        0.0860022164024663       0.00751375419621145
        0.0871166286741767      0.000358708591819956
        0.0871724982351543     -3.53732281678005e-06
        0.0871719526702084      1.50893647070057e-09

Printouts

[vBO,dV,tOF] = BurnoutVelocity( lv );
range = vBO/pi*cos((pi/2-gammaFinalDes)/2)*sum(tOF);

fprintf(1,'Predicted burnout velocity: %f km/s\n',vBO);
fprintf(1,'   Actual burnout velocity: %f km/s\n',vFinal);

fprintf(1,'Predicted range: %f km\n',range);
fprintf(1,'   Actual range: %f km\n',x(1));

kPlot = 1:k;
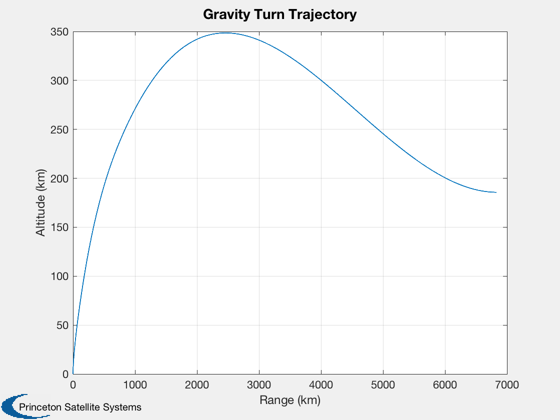
Plot2D(xPlot(1,kPlot),xPlot(2,kPlot),'Range (km)','Altitude (km)','Gravity Turn Trajectory');
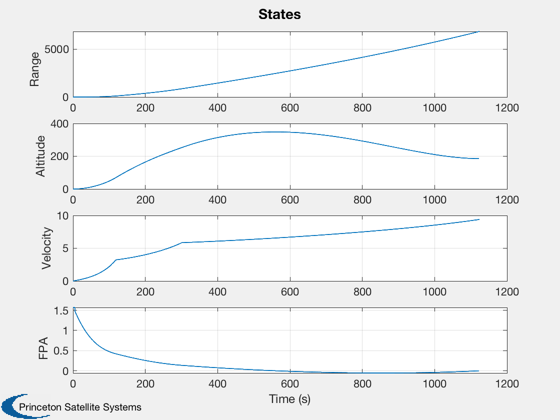
Plot2D(dT*kPlot,xPlot(1:4,kPlot),'Time (s)',{'Range','Altitude','Velocity','FPA'},'States');
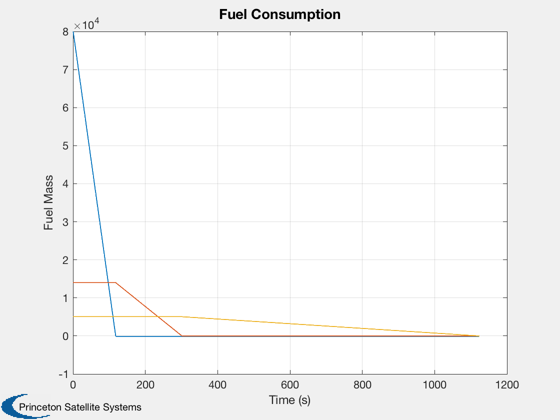
Plot2D(dT*kPlot,xPlot(5:end,kPlot),'Time (s)','Fuel Mass','Fuel Consumption');


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Predicted burnout velocity: 10.604871 km/s
   Actual burnout velocity: 9.395955 km/s
Predicted range: 2680.451342 km
   Actual range: 6840.663930 km

Published with MATLAB® R2019a