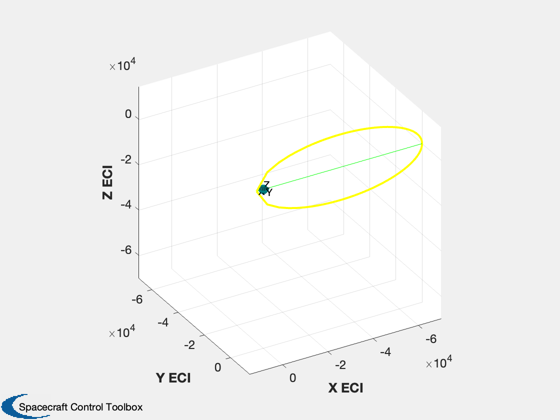
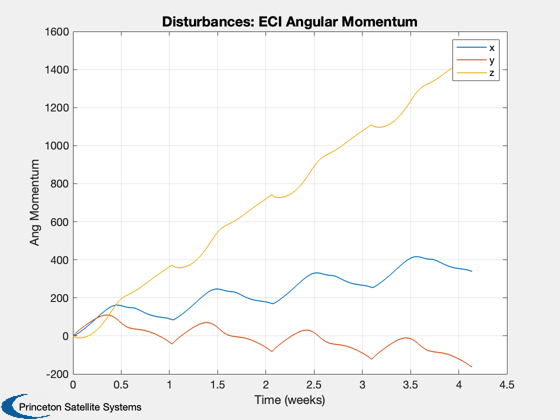
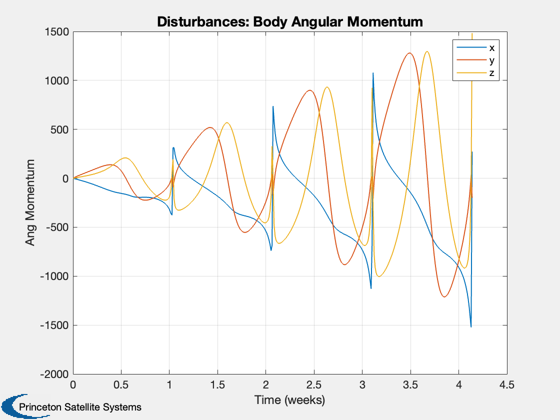
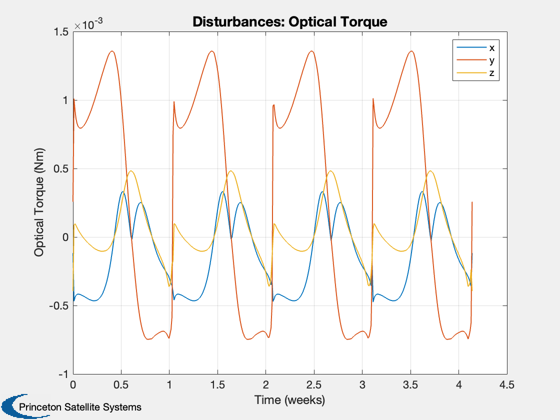
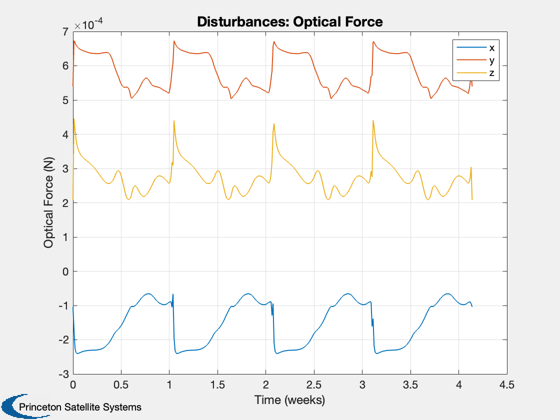
Disturbance analysis for Gateway

Loads GatewaySimple.mat. Can choose between sun pointing or the orientation which minimizes the gravity gradient disturbance torque. You can compare the results to the full model, Gateway.mat, which will run much, much more slowly

See also: Constant, DrawSCPlanPlugIn, Disturbances, Date2JD, Period, RVOrbGen, PltOrbit, SunV1, UMinGG, Q2Mat, U2Q, Figui

Contents

%--------------------------------------------------------------------------
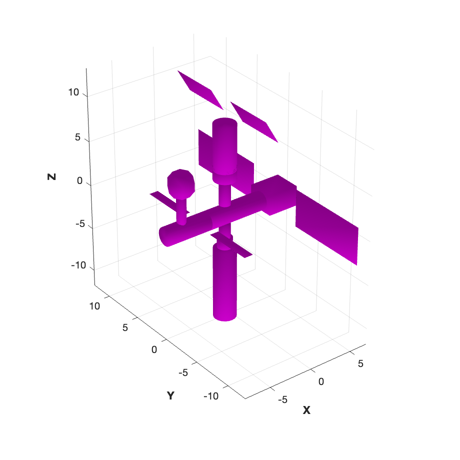
%  	Copyright (c) 2022 Princeton Satellite Systems, Inc.
%   All rights reserved.
%   Since 2023.1
%--------------------------------------------------------------------------

% Plot
sunPointing = false;

% Constants
mu        = Constant('mu moon');
rM        = Constant('equatorial radius moon');

% Gateway
rA        = 70000;
rP        =  3000;
[a, e]    = RPRA2AE( rP, rA );
el        = [a pi/2 0 0 e 0];

% Load the model and display it
% g = load('Gateway.mat');       % full model with >80,000 faces
g = load('GatewaySimple.mat'); % simple model with <500 faces

% The body inertia is used for gravity gradient
inertia = [1.6406e+06  -8.6764e+04  -4.7583e+03;...
          -8.6764e+04   9.9031e+05  -8.5474e+02;...
          -4.7583e+03  -8.5474e+02   1.8093e+06];

cM = [ -3.1182e-04; 4.2778e-05; -1.5026e-05];
g.component(1).mass = struct('mass',40000,'inertia',inertia,'cM',cM);
g.body(1).mass = g.component(1).mass;

DrawSCPlanPlugIn(g);

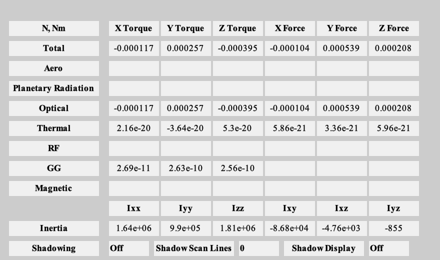
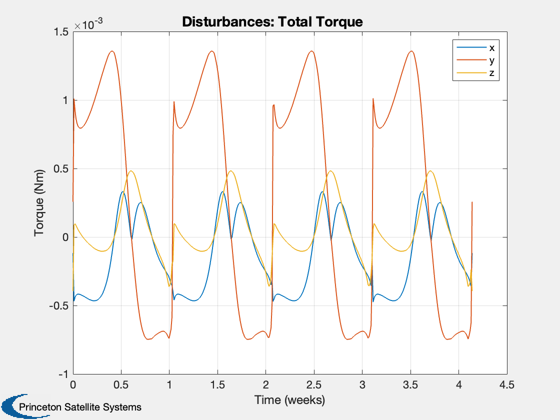
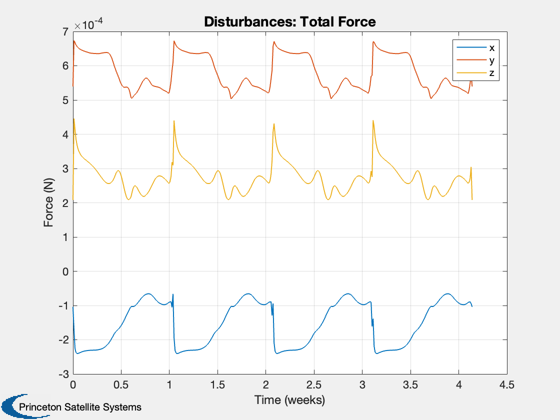
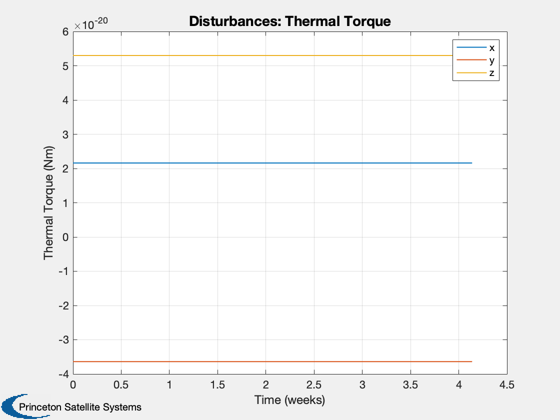
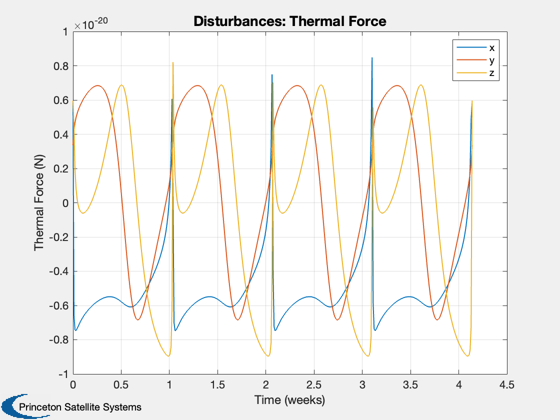
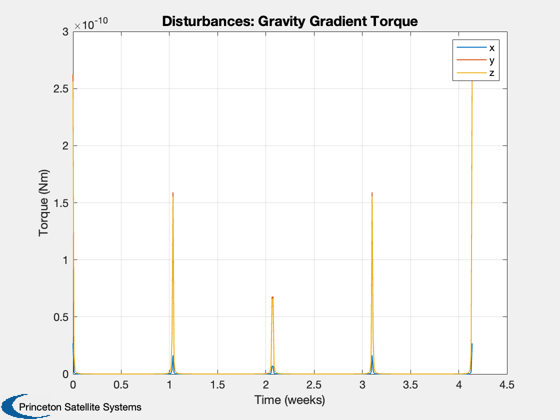
Perform the disturbance analysis

e = Disturbances( 'defaults' );

% Script control
nOrbits        = 4;
e.computeAero  = false;
e.computeMag   = false;
e.computePR    = false;
nSamp          = 400;
jD0            = Date2JD([2024 2 2]);

% Orbit
period         = Period( a, mu );
t              = linspace(0,nOrbits*period,nSamp);
e.tSamp        = t(2);
[e.r,e.v]      = RVOrbGen(el,t,[],mu);
e.mu           = mu;
e.planetRadius = 1738;
e.units        = 'm';
PltOrbit( el, jD0, [], 'moon' );

% Generate the transformation matrices
jD = jD0 + t/86400;
uSun = SunV1(jD);
if( sunPointing )
  for k = 1:length(jD)
    g.body(1).bHinge(k).b = Q2Mat(U2Q(uSun(:,k),[1;0;0]))';
  end
else
  u = UMinGG(inertia );
  for k = 1:length(jD)
    g.body(1).bHinge(k).b = Q2Mat(U2Q(Unit(e.r(:,k)),u))';
  end
end

% Initialize the disturbance model
hD = Disturbances( 'init', g, e );

% Run the analysis
Disturbances( 'run', g, e, hD );
Figui;


%--------------------------------------

% $Id: 7e5ae5653a7dfcaa422c904a95229f87d59ed3d0 $

Published with MATLAB® R2023b