Demonstrate lunar lander guidance

Simulates in the moon fixed frame.

See also: RHSRVPlanetFixed, Constant, MoonRot, El2RV, LoadLunarTopography, AltitudeSH, TimeLabl, RK4

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2015 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2016.1
%--------------------------------------------------------------------------

clear q

User inputs

thrust    = 45040;    % 45040; % N
iSp       = 311;   % s
g         = 9.806; % m/s^2
massOrbIn = 30*thrust/(iSp*g);
h0        = 15;   % Inital altitude (km)
tEnd      = 2*86400;	% End time (sec)
dT        = 5;    % Time step (sec)
massFuel	= 8200 - massOrbIn; % Fuel (kg) (Lunar Module)
inc       = pi/2; % Orbit inclination (rad)
jD0       = Date2JD([2017 4 15 0 0 0]);
nH        = 72; % Number of harmonics in topology model
rotModel  = 'mean';

Set up the simulation

% Constant
kmToM = 1000;

% Default data
d                       = RHSRVPlanetFixed;
d.rVStruct.mu           = Constant('mu moon');
d.rVStruct.jD0          = jD0;
d.rVStruct.massDry      = 10334 - massFuel + 4700; % Includes ascent stage
d.rVStruct.bFun         = @MoonRot;
d.rVStruct.bFunData     = rotModel;
d.dataFunThrust.uE      = iSp*g;
d.dataFunThrust.thrust	= thrust;

% Initial orbit
rMoon     = Constant('equatorial radius moon');
el        = [rMoon + h0; inc; 0; 0; 0; 0]; % Polar orbit
[r,v]     = El2RV(el,[],d.rVStruct.mu);

% Transform into moon fixed coordinates
[g,omega]	= MoonRot( jD0, rotModel );
v         = g*(v - Cross(omega,r));
r         = g*r;

% Lhnar topography
[s,c]     = LoadLunarTopography( nH );

% The initial state
x         = [r;v;massFuel];

Simulate

n   = ceil(tEnd/dT);
xP  = zeros(length(x)+1,n);
t   = 0;

for k = 1:n

  % Altitude
  h = AltitudeSH( x(1:3), s, c, nH );

  %  Control
  d.dataFunThrust.uThrust = -Unit(x(4:6));

  % Plotting
  xP(:,k)	= [x;h];

  % Terminate at zero altitude
  if( h <= 0 )
    break;
  end

  % Propagate one step
  x = RK4( @RHSRVPlanetFixed, x, t, dT, d );
  t = t + dT;

end

% Account for the termination of the sim due to altitude
xP = xP(:,1:k);

Plot the results

[t,tL]  = TimeLabl((0:(k-1))*dT);
yL      = {'x (km)'     'y (km)'      'z (km)' ...
          'v_x (km/s)', 'v_y (km/s)', 'v_z (km/s)' ...
          'Fuel (kg)' 'h (km)'};

% This is to make the plots look nice
k       = xP(7,:) < 0;
xP(7,k) = 0;
k       = xP(8,:) < 0;
xP(8,k) = 0;

% 2D plots
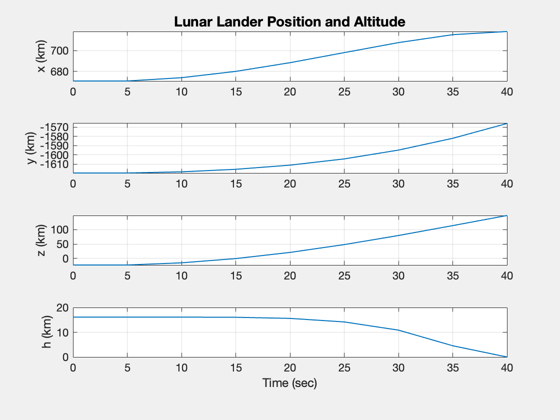
k = [1:3 8];
Plot2D( t, xP(k,:), tL, yL(k), 'Lunar Lander Position and Altitude');

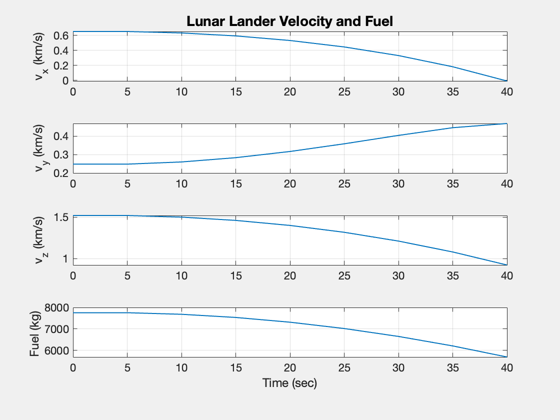
k = 4:7;
Plot2D( t, xP(k,:), tL, yL(k), 'Lunar Lander Velocity and Fuel');

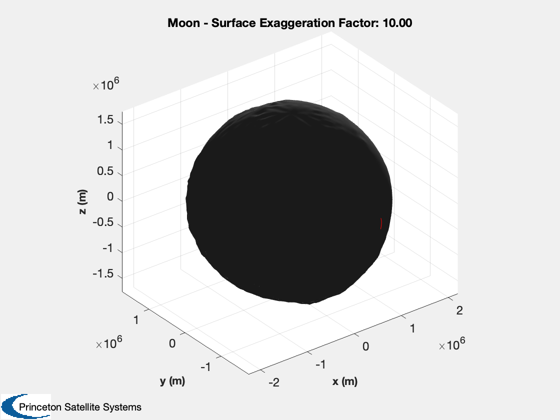
% 3D plots
[q.r, q.lambda, q.theta]	= RSHMoon; % Clementine model
q.rEq                     = 1738000; % m
q.name                    = 'Moon';
PlanetWithTerrain( q, 10 );
hold on
plot3(xP(1,:)*kmToM,xP(2,:)*kmToM,xP(3,:)*kmToM,'r')

%--------------------------------------
% PSS internal file version information
%--------------------------------------

% $Id: cda1628c4f4daec6b932811c9c69067249f94ce5 $

Published with MATLAB® R2024a