Test Fault Diagnosis using online approximators.

This script replicates the example in the referenced paper.

Since version 9.
----------------------------------------------------------------------
References: Demetriou, M. A. and M. M. Polycarpou. "Incipient Fault
           Diagnosis of Dynamical Systems Using Online Approximators."
           IEEE Trans. Automatic Control, Vol. 43, No. 11, Nov. 1998,
           pp. 1612-1616.
----------------------------------------------------------------------
See also Plot2D, RK4, NonlinearEstimator, NonlinearSpringFault,
OnlineApproximator, delta
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2002 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

clear d; clear dEst;

dT   = 0.1;

tEnd = 60;

nSim = tEnd/dT;

yPlot = zeros(4,nSim);
qPlot = zeros(19,nSim);
t     = (0:(nSim-1))*dT;

y     = [0.5;0.1];

Spring data

%------------
d.m      = 1;
d.k0     = 0.5;
d.c0     = 0.5;
d.a      = 1;
d.rho    = 0.1;
d.tFail  = 10;
d.f      = 5;
d.omegaF = 1.0;

delta    = d.k0*d.a^2;

Estimator states

%-----------------
nP               = 19;
yEst             = [0;0;zeros(nP,1)];
dEst.plant.k0    = d.k0;
dEst.plant.c0    = d.c0;
dEst.plant.m     = d.m;
dEst.est.k       = 0.55;
dEst.est.c       = 5;
dEst.oA.sigma    = 0.5/sqrt(log(2));
dEst.oA.c        = linspace(-9,9,nP)';
dEst.thetaMax    = 100;
c                = dEst.est.c;
k                = dEst.est.k;
dEst.gamma       = 100*max([(sqrt(c^2 + 4*d.m*k) - c)/(2*k) d.m/c]);
dEst.dT          = dT;
dEst.f           = d.f;

for k = 1:nSim
  yEst       = NonlinearEstimator( yEst, y, t(k), dEst );
  f          = NonlinearSpringFault( y, t(k), d );
  fOLA       = -OnlineApproximator( y(1), yEst(3:end), dEst.oA );
  yPlot(:,k) = [y(1);yEst(1);f;fOLA];
  qPlot(:,k) = yEst(3:end);
  y          = RK4('NonlinearSpring', y, dT, t(k), d );
end

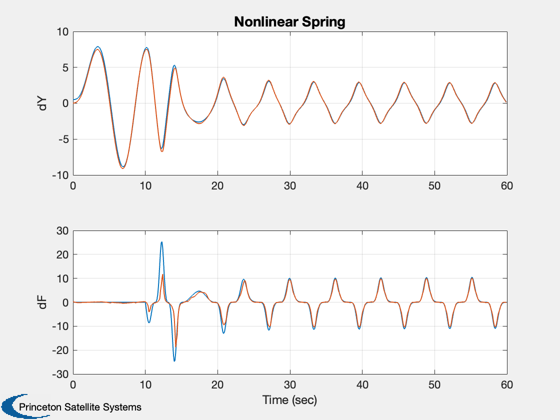
We are plotting y, yDot and the fault which is the nonlinear

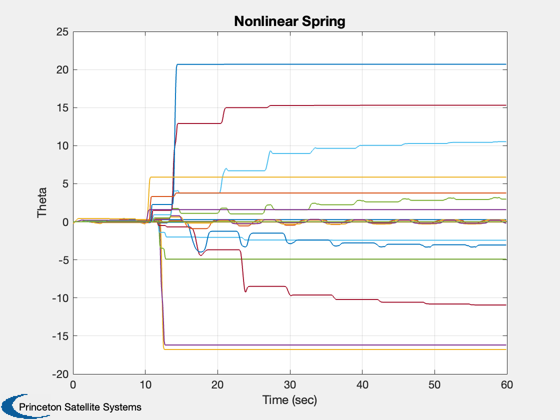
Plot2D( t, yPlot, 'Time (sec)',['dY';'dF'],'Nonlinear Spring','lin',{'[1 2]';'[3 4]'})
Plot2D( t, qPlot, 'Time (sec)','Theta','Nonlinear Spring')


%--------------------------------------
% PSS internal file version information
%--------------------------------------

% $Id: 8e5136ccf49aa9eaf06d68af3b954e78d3ac679f $

Published with MATLAB® R2022b