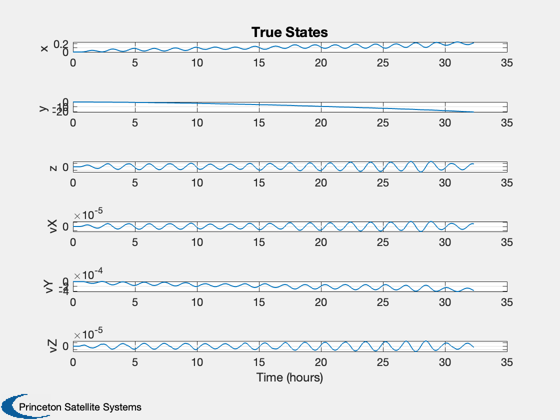
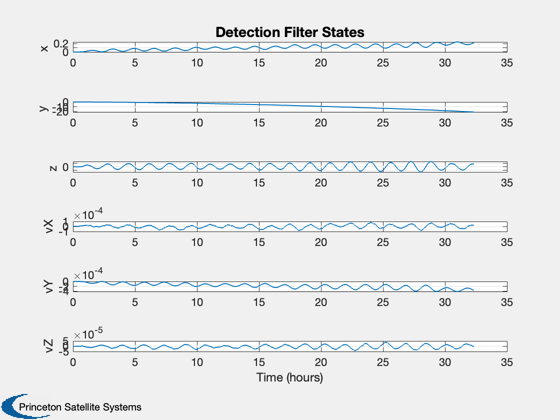
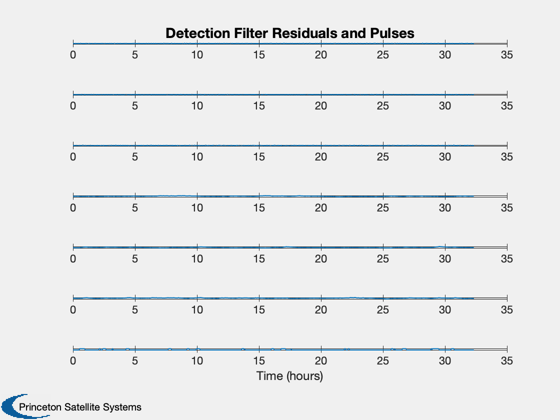
Demonstrate an orbit detection filter with random thrust pulses.

This filter will detect measurement failures and actuator failures. A single thruster is assumed and it is assumed that each measurement of x, y, z and velocity is independent.

Since version 10.
-------------------------------------------------------------------------
See also @statespace/statespace.m, C2DZOH, CToD, Plot2D, TimeLabl,
Unit, DetectionFilterBuild, DetectionFilterUnnormalized, LinOrb, Period
-------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2002 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Setup

if( exist('LinOrb') )
  [a,b,c,d] = LinOrb( [], 1 );
else
  a       = [ zeros(3), eye(3); diag([3 0 -1]), [0 2 0;-2 0 0;0 0 0] ];
end

if( exist('Period') )
  rNom    = 7000;
  p       = Period(rNom);
else
  p       = 5828.51668009113; % sec
end

nOrbits   = 20;
dT        = 100;

% Random pulse train; rand (0-1) is used with these thresholds to create pulses.
uRandOn   = 0.02; % threshold to start a pulse (rand < uRandOn)
uRandOff  = 0.1;  % threshold to continue a pulse (rand > uRandOff)

wo        = 2*pi/p;
dT        = wo*dT;
c         = eye(6);
d         = zeros(6,1);
bV        = Unit([0;1;1]);
b         = [0;0;0;bV]; % Only one thruster pointing in an arbitrary,
                        % Hill's equation fixed, direction.

nSim      = floor(nOrbits*p*wo/dT); % 4 years
xPlot     = zeros(12,nSim);
rPlot     = zeros(6,nSim);

x         = zeros(6,1);
thrust    = 0.001; % N
mass      = 100; % kg
aMax      = thrust*0.001/mass; % km/sec^2
uMax      = aMax/wo^2; % km

% Set up the state space model
%-----------------------------
states       = {'x' 'y' 'z' 'vX' 'vY' 'vZ'};
inputs       = {'u'};
outputs      = states;
g            = statespace( a, b, c, d, 'Linear Orbit', states, inputs, outputs );

d            = DetectionFilterBuild( g, -0.25 );

% Set up the detection filter
%----------------------------
[aX, d.d]    = C2DZOH( a, d.d, dT );

% Convert plant to discrete time
%-------------------------------
[a, b]       = C2DZOH( a, b, dT );
d.g          = CToD( g, dT, 'z' );

xE           = x;

% Add noise
%----------
pos1Sigma    = 10;
vel1Sigma    = pos1Sigma*wo;
y1Sigma      = [pos1Sigma*ones(3,1);vel1Sigma*ones(3,1)]*1e-3; % Convert to km
bias         = [1;1;1;wo;wo;wo];
bias         = zeros(6,1);
rD           = zeros(6,1);
u            = zeros(1,size(rPlot,2));

Simulate

%---------
for k = 1:nSim
  xPlot(:,k)   = [x;xE];
  rPlot(:,k)   = rD;
  yMeas        = c*x + y1Sigma.*randn(6,1) + bias;
  [rD, xE]     = DetectionFilterUnnormalized( d, yMeas, 0, xE );

  % Create a random pulse train
  %----------------------------
  if( k > 1 )
    if( u(k-1) == 0 )
      % initiate a new pulse
      if( rand < uRandOn )
        u(k) = uMax;
      end
    else
      % extend an existing pulse
      if( rand > uRandOff )
        u(k) = uMax;
      end
    end
  end
  x = a*x + b*u(k);
end

Plot

% Convert velocity to km/sec
%---------------------------
xPlot([4:6 10:12],:) = xPlot([4:6 10:12],:)*wo;

% Generate reasonable time labels
%--------------------------------
[t,tL] = TimeLabl( (0:(nSim-1))*dT/wo );

yL = {'x', 'y', 'z', 'vX', 'vY', 'vZ' };
Plot2D( t, xPlot(1:6,:), tL, yL,'True States','lin' );
Plot2D( t, xPlot(7:12,:), tL, yL,'Detection Filter States','lin' );

yL = {'x', 'y', 'z', 'vX', 'vY', 'vZ', 'u' };

Plot2D( t, [rPlot;u], tL, yL,'Detection Filter Residuals and Pulses' );


%--------------------------------------
% PSS internal file version information
%--------------------------------------

% $Id: 5b6830dc2c1dd8a95cc4794c4e5738fd8725108a $

Published with MATLAB® R2022b