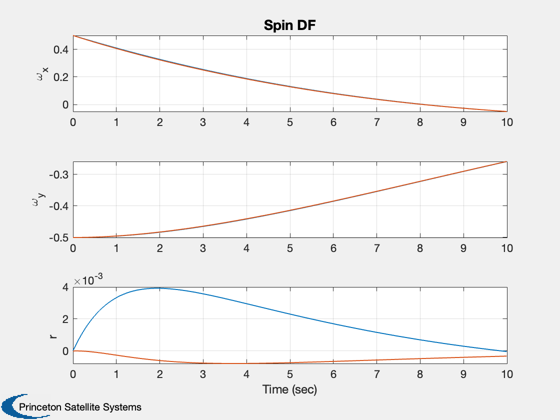
Demonstrate a detection filter for a spinning spacecraft.
This filter will detect measurement failures and actuator failures This function uses an analytical derivation of a detection filter which is feasible for this simple system. For linear time invariant systems the detection filter gain matrix is a constant.
Since version 9. ------------------------------------------------------------------------- See also C2DZOH, Plot2D -------------------------------------------------------------------------
Contents
%-------------------------------------------------------------------------- % Copyright (c) 2006-2008 Princeton Satellite Systems, Inc. % All rights reserved. %--------------------------------------------------------------------------
Filter and plant parameters
%----------------------------
c = 0.1; k = 0.1;
a = [-0.9*c k;-k -c]; b = eye(2);
aE = [-c k;-k -c];
lam = -1;
d = [-c-lam -k;k -c-lam];
Set up the simulation
%----------------------
nSim = 1000; dT = 0.01;
xPlot = zeros(6,nSim);
x = [0.5;-0.5]; xE = x;
Discretize the plant and filter
%-------------------------------- [aE,d] = C2DZOH(aE,d,dT); [a,b] = C2DZOH(a,b,dT); for k = 1:nSim r = x - xE; xPlot(:,k) = [x;xE;r]; x = a*x; xE = aE*xE + d*(x - xE); end Plot2D( (0:(nSim-1))*dT, xPlot, 'Time (sec)', {'\omega_x' '\omega_y' 'r'},... 'Spin DF','lin',{'[1 3]';'[2 4]';'[5 6]'} ); %-------------------------------------- % PSS internal file version information %-------------------------------------- % $Id: caee61473c7d146928bf3ef6a75cb776ab3c495b $