Analysis of approach orbits to Alpha Centauri binary system

Alpha Centauri A-B system is in XY plane
The spacecraft approaches from Earth at:
    16.7 deg elevation angle to the plane
  -122.2 deg azimuth angle (measured from perigee of B's orbit about A)

Begin approach with a hyperbolic orbit around A.
You may use this as an initial condition to numerically integrate RHS
to see effect of B disturbance. Use RHSAlphaCentauriMission.

Since version 10.
------------------------------------------------------------------------
See also AlphaCentauriMissionAnalysis
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 2011 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

Constants

day     = 86400;
au      = Constant('au');
muScale = day^2 / au^3;
muE   = 3.98600436e5 * muScale;
muS   = Constant('mu sun') * muScale;
muA   = 1.10*muS;
muB   = 0.93*muS;

position of Alpha Centauri A with respect to Earth

rA      = HMS2Rad(14,39,36.5);                            % right ascension
dec     = DMS2Rad(-60,50,02.3);                           % declination
uPosAC  = [cos(rA)*cos(dec);sin(rA)*cos(dec);sin(dec)];   % unit vector
distAC  = 63241.1;                                        % distance (AU)
posAC   = uPosAC*distAC;                                  % position vector

orbit of binary star system (B about A)

sma = 17.57*1.338;  % AU
ecc = 0.5179;
inc = 79.2*pi/180;
raan = 204.85*pi/180;
prg = 241.65*pi/180;
elB = [sma, inc, raan, prg, ecc, 0];

rotation matrix from local perifocal to standard inertial frame

Here, xy is the Sun-Earth ecliptic plane.

cMat = CP2I( inc, raan, prg );

position of star B about star A in perifocal frame of Alpha-Centauri

w0 = 0;
w = w0 + linspace(0,2*pi);
rBMag = sma*(1-ecc^2) ./ (1+ecc*cos(w));
rBA = [ rBMag.*cos(w); rBMag.*sin(w); zeros(size(w)) ];

position of Earth in Alpha-Centauri perifocal frame

posE = cMat'*-posAC;
uPosE = Unit(posE);

angular representation of Earth position

elev = asin( posE(3) / Mag(posE) );   % elevation measured to +Z from XY
azim = atan2( posE(2), posE(1) );     % azimuth measured towards +Y from +X

compute gravitational force to A, B, along line

n = 1e3;
distX = logspace(-1,2,n);
rSA = [uPosE(1)*distX; uPosE(2)*distX; uPosE(3)*distX];
rSB = rSA - repmat(rBA(:,1),1,n);
gA = zeros(3,n);
gB = zeros(3,n);
for i=1:n
  gA(:,i) = -muA*rSA(:,i)/Mag(rSA(:,i))^3;
  gB(:,i) = -muB*rSB(:,i)/Mag(rSB(:,i))^3;
end

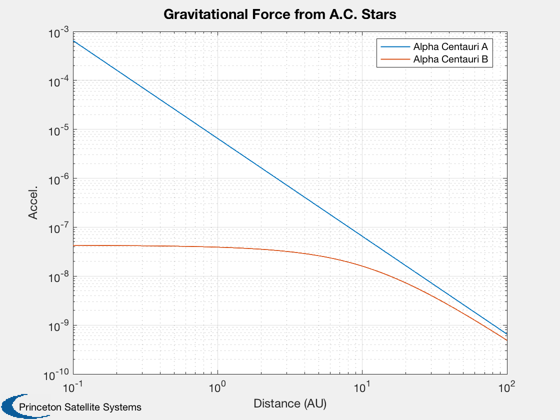
Plot the gravitational force from both stars

Plot2D(distX,[Mag(gA);Mag(gB)]*au/day^2,'Distance (AU)','Accel.','Gravitational Force from A.C. Stars','log',[],[],[],[],[],{{'Alpha Centauri A','Alpha Centauri B'}})

hyperbolic approach orbit

e   = 1/cos(elev);
i   = pi/2;
ra  = azim + pi;
w   = 0;
M   = 0;
a   = 1/(1-e);
elH = [a,i,ra,w,e,M];

Keplerian orbit for hyperbolic approach over 10 Earth-years

t = (-5 : .01 : 5)*365.25;
r = RVOrbGen([a,i,ra,w,e,M],t,[],muA);

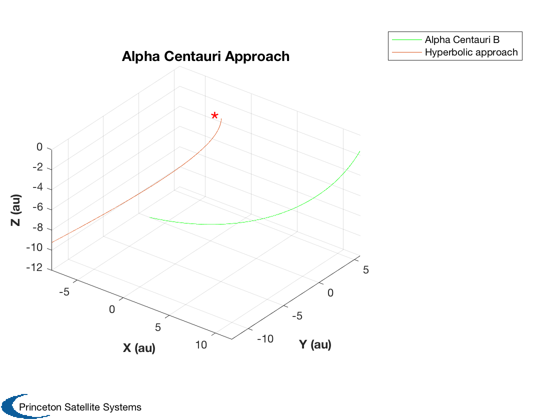
Plot approach path

rB = RVOrbGen( elB, t, [], muA );
[h, hL] = Plot3D(rB,'X (au)', 'Y (au)', 'Z (au)','Alpha Centauri Approach');
set(hL,'linewidth',0.5,'color',[0 1 0]);
hold on
rk = RVOrbGen(elH,t,[],muA);
plot3(rk(1,:), rk(2,:), rk(3,:))
set(gca,'zlim', [-12 0]);
text(0,0,0, '*','color',[1 0 0],'fontsize',24)
legend('Alpha Centauri B','Hyperbolic approach');

% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2019a