Contents

Design a roll/yaw controller using a double pivot

See also C2DZOH, QCR, Plot2D, TimeLabl, Geo

%--------------------------------------------------------------------------
%   Copyright (c) 1996 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 1.
%   Formerly TRYDP.m
%--------------------------------------------------------------------------

Constants

%----------
radToDeg = 180/pi;

Disturbance magnitudes

%-----------------------
tImp     = [0;0];
tStep    = [10e-6;10e-6];
tOrbRate = [0;0];

Orbit rate

%-----------
wo = Geo;

Momentum

%---------
hW = 500;

Plant [roll;yaw]

%-----------------
a  = [0 wo;-wo 0];
bC = -eye(2);  % u = [wX;wZ] where alpha is the x-angle and beta is the z-angle
bD = [0 -1;1 0]/hW;

Platform plant

%---------------
aP = [0 wo;-wo 0];
bP = eye(2);

Design the controller

%-----------------------
kC = QCR( a, bC, 1.e-7*[1 0;0 1], eye(2));

DispWithTitle(kC,'Gains');

disp('Closed loop eigenvalues')
s = eig(a - bC*kC);
DispWithTitle(s,'Eigenvalues');

Gains
   1.0e-03 *
  -0.316227766016838  -0.000000000000000
   0.000000000000000  -0.316227766016838
Closed loop eigenvalues
Eigenvalues
   1.0e-03 *
 -0.316227766016838 + 0.072921158552912i
 -0.316227766016838 - 0.072921158552912i

Control period

%---------------
dT = 100;

Convert to discrete time

%-------------------------
[aX,bD] = C2DZOH(a, bD,dT);
[a, bC] = C2DZOH(a, bC,dT);
[aP,bP] = C2DZOH(aP,bP,dT);

Simulate a step response

%-------------------------
nSim   = 864;
x      = zeros(2,1);
xP     = zeros(2,1);
xPlot  = zeros(2,nSim);
aPlot  = zeros(2,nSim);
uPlot  = zeros(2,nSim);
tPlot  = zeros(1,nSim);
t      = 0;

for k = 1:nSim

  % Controller
  %-----------
  uC = -kC*x;

  % Disturbance
  %-----------
  c  = cos(wo*t);
  s  = sin(wo*t);
  uD = tImp + tStep + [c s;-s c]*tOrbRate;

  % Plotting
  %---------
  xPlot(:,k)  = x;
  aPlot(:,k)  = xP;
  uPlot(:,k)  = uD;
  tPlot(k)    = t;

  % Update the state
  %-----------------
  x  = a*x   + bC*uC + bD*uD;
  xP = aP*xP + bP*uC;
  t  = t + dT;

  tImp = [0;0];

end

[tPlot,xLbl] = TimeLabl(tPlot);

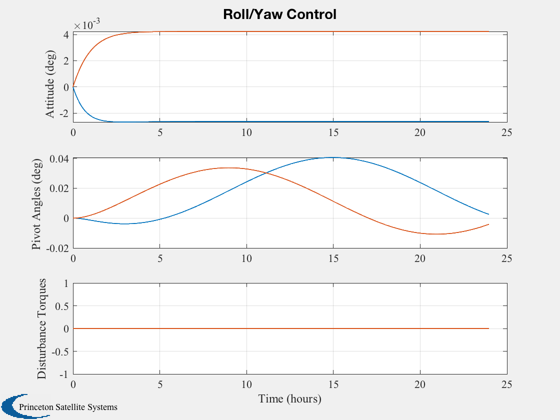
Plots

%------
yLbl = ['Attitude (deg)     ';...
        'Pivot Angles (deg) ';...
		    'Disturbance Torques'];
Plot2D(tPlot,[xPlot*radToDeg;aPlot*radToDeg;uPlot],xLbl,yLbl,'Roll/Yaw Control','lin',['1:2';'3:4';'5:6'])


%--------------------------------------

Published with MATLAB® R2019a