Contents

Least Squares Optimization

This demonstrates a least squares solution for lunar landing in 3D. The solution is in the moon fixed frame.

%--------------------------------------------------------------------------
%   Copyright (c) 2014-2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2016.1
%--------------------------------------------------------------------------

Constants

muMoon            = 4904.8695; % km^3/sec^2
rMoon             = 1738; % km

User inputs

n                 = 30;    % Number of steps
h                 = 15;   % Initial altitude (km)
m0                = 100;  % Dry mass (kg)
thrustMax         = 450; % N
uGS               = [0;0;-1];
tMax              = 400;
uE                = 310*9.806;

% Define the landing point
lat               = 8*pi/180; % rad
lon               = 0; % rad
alt               = 0; % km

Set up the optimization

r                 = rMoon + h;
d                 = RHSPlanet3D;

% Iterate to find the mass of the fuel and maneuver duration
% The mass of fuel will be updated for the nonlinear simulation
% based on the optimization results
mF                = 0;
for k = 1:10
	dV	= thrustMax*tMax/(m0+mF);
  mF	= m0*(exp(dV/uE) - 1);
end

u                 = sqrt(muMoon/r); % Orbital velocity
g                 = muMoon/rMoon^2; % Gravity at the lunar surface
d                 = RHSPlanet3D;
d.n               = n; % Number of steps
d.m0              = m0; % Dry mass

% Specify the target
xTarget     = LunarLandingTargetState( lat, lon, alt );

fprintf(1,'Target latitude  %8.2f deg\n',lat*180/pi);
fprintf(1,'Target longitude %8.2f deg\n',lon*180/pi);
fprintf(1,'Target altitude  %8.2f deg\n', alt);
fprintf(1,'Maneuver time    %8.2f sec\n',tMax);
fprintf(1,'Mass dry         %8.2f kg\n',m0);
fprintf(1,'Mass fuel        %8.2f kg\n',mF);
fprintf(1,'Velocity change  %8.2f m/s\n',dV);
fprintf(1,'Maximum thrust   %8.2f N\n\n',thrustMax);

d.thrustMax = thrustMax;
x0          = [r;0;0;0;0;u;mF]; % Initial state vector
dT          = tMax/n;

% This sets the linearized equations to use a constant gravity
x = zeros(6,n);
for k = 1:n
  x(:,k) = x0(1:6);
end

% Maximum acceleration is the maximum acceleration with full fuel load
dO       = d;
dO.m0    = 1;
[aC,bC]  = OrbitStateMatrices( x, xTarget, dT, dO );

Target latitude      8.00 deg
Target longitude     0.00 deg
Target altitude      0.00 deg
Maneuver time      400.00 sec
Mass dry           100.00 kg
Mass fuel           48.85 kg
Velocity change   1209.10 m/s
Maximum thrust     450.00 N

Least squares solutions

q        = pinv(aC)*bC;

% Generate acceleration vectors
u = zeros(3,n);
for k = 1:n
	i       = 3*k-2:3*k;
	u(:,k)  = q(i);
end

Compute the fuel mass required for the landing

accel = Mag(u);
mFuel = FuelMassFromAccel( accel, dT*ones(1,n), d.m0, uE );

fprintf(1,'Mass of fuel required %12.4f kg\n',mFuel);

Mass of fuel required      82.9763 kg

Simulate

dRHS	= d;
x     = x0;
xP    = zeros(10,n+1);
x(7)  = mFuel;
for k = 1:n
  thrust        = u(:,k)*(d.m0 + x(7));
	dRHS.thrust   = Mag(thrust);
	dRHS.uThrust  = Unit(thrust);
	xP(:,k)       = [x;thrust];
	x             = RK4('RHSPlanet3D',x,dT,0,dRHS);
end

xP(:,k+1) = [x;thrust];
h         = Mag(xP(1:3,:)) - rMoon;
v         = Mag(xP(4:6,:));
tMag      = Mag(xP(8:10,:))./(d.m0 + x(7));
gS        = GlideSlope( uGS, xTarget(1:3), xP(1:3,:), rMoon );

Plot

Labels

yL = {'x (km)' 'y (km)' 'z (km)'...
      'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)',...
      'T_x (N)' 'T_y (N)' 'T_z (N)',...
      'h (km)', '|v| (km/s)' '\phi (deg)' 'm_f (kg)'  '|a| (m/s^2)' };

% Convert time to reasonable units
[t, tL] = TimeLabl((0:n)*dT);

% Plot
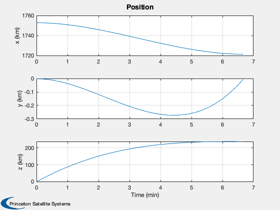
Plot2D( t, xP(1: 3,:),        tL, yL( 1: 3),        'Position');
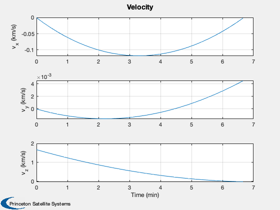
Plot2D( t, xP(4: 6,:),        tL, yL( 4: 6),        'Velocity');
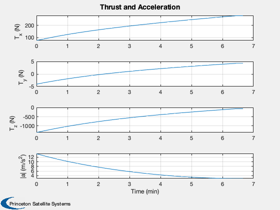
Plot2D( t, [xP(8:10,:);tMag],	tL, yL( [7 8 9 14]),  'Thrust and Acceleration');
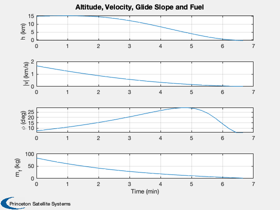
Plot2D( t, [h;v;gS;xP(7,:)],	tL, yL(10:13),        'Altitude, Velocity, Glide Slope and Fuel');


%--------------------------------------

Published with MATLAB® R2020a