Test fmincon against an analytical solution for the linear tangent law

The test is for a lunar landing in 2D. The surface is assumed flat. The acceleration is constant.

Requires fmincon from the MATLAB Optimization Toolbox.

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2015 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2016.1
%--------------------------------------------------------------------------

if( ~HasOptimizationToolbox )
  error('You need the MATLAB optimizaton toolbox to run this script.');
end

Parameters

muMoon        = Constant('mu moon');
rMoon         = Constant('equatorial radius moon');
d             = struct;
d.u           = sqrt(muMoon/rMoon); % Orbit velocity
d.g           = muMoon/rMoon^2; % Gravity
d.h           = 10; % Altitude (km)
d.n           = 100; % Number of increments
d.a           = 3*d.g; % Engine acceleration
d.x           = [0;d.h;-d.u;0]; % Initial state
printFigures	= 0;
algorithm     = 'interior-point';

% Find the thrust direction angles
[beta, t, tMin]   = BilinearTangentLaw( d.u, d.g, d.a, d.h, d.n );
fprintf(1,'Analytical minimum time %12.4s sec\n',tMin);

% We don't want the last beta since the vehicle is on the ground
beta        = beta(1:end-1);
d.n         = d.n-1;

% Do this to get a landing
beta        = fliplr(beta);

% Simulate the landing
Simulate2DLanding( t, beta, d, 'Analytical' );

Analytical minimum time   3.6651e+02 sec

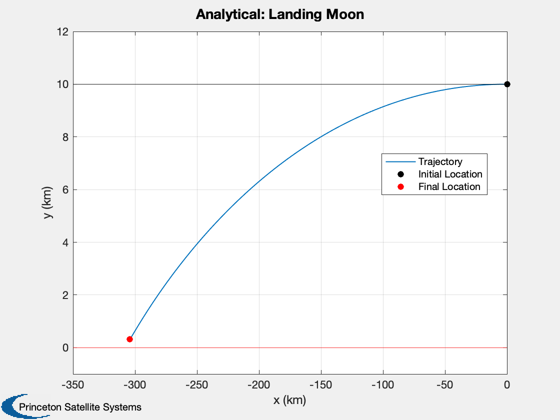
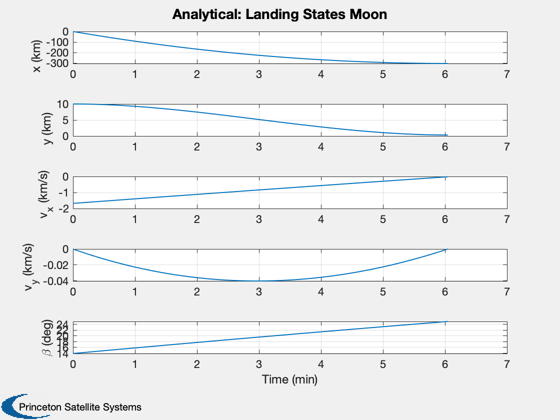
Now repeat with fmincon

% fmincon options
if( verLessThan('matlab', 'R2014b') )
  opts      = optimset( 'Display','iter-detailed',...
                        'TolFun',0.6,...
                        'TolCon',1e-5,...
                        'MaxFunEvals',100000);
else
  opts      = optimset( 'Display','iter-detailed',...
                        'TolFun',0.6,...
                        'algorithm',algorithm,...
                        'TolCon',1e-5,...
                        'MaxFunEvals',100000);
end

% The cost is time, which is a decision variable
% The cost is the time to reach the final state vector
costFun   = @(x) LandingCost2D(x,d);

% The numerical integration of the state is in the constraint function
constFun	= @(x) LandingConst2D(x,d);

% The final state vector is [x;0;0;0];
% We don't care what x is since we can always start the descent at the
% appropriate time.

% First guess for the time decision variable
dT        = t(2:end) - t(1:end-1);

% Do this to get a reasonable first guess but not exact
beta      = 1.2*beta;

% The decision variables are acceleration angle and time increment
x0        = [beta';dT'];

% Lower and upper bounds
lB        = zeros(length(x0),1);
uB        = [(pi/2)*ones(length(dT),1);100*ones(length(dT),1)];

% Find the optimal decision variables.
x         = fmincon(costFun,x0,[],[],[],[],lB,uB,constFun,opts);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0     199    3.665056e+02    1.928e+01    2.341e-03
    1     398    3.654524e+02    1.263e-01    2.756e-01    7.165e-01
    2     597    3.665039e+02    1.949e-04    1.000e-01    1.139e-01
    3     796    3.665057e+02    5.599e-06    2.831e-03    3.457e-03

Optimization completed: The relative first-order optimality measure, 2.830935e-03,
is less than options.OptimalityTolerance = 6.000000e-01, and the relative maximum constraint
violation, 2.903503e-07, is less than options.ConstraintTolerance = 1.000000e-05.

Set up the simulation

beta      = x(1:d.n)';
dT        = x(d.n+1:2*d.n);
t         = zeros(1,length(dT));
for k = 2:d.n+1
  t(k) = t(k-1) + dT(k-1);
end

% Simulate the landing
Simulate2DLanding( t, beta, d, 'FMinCon' );

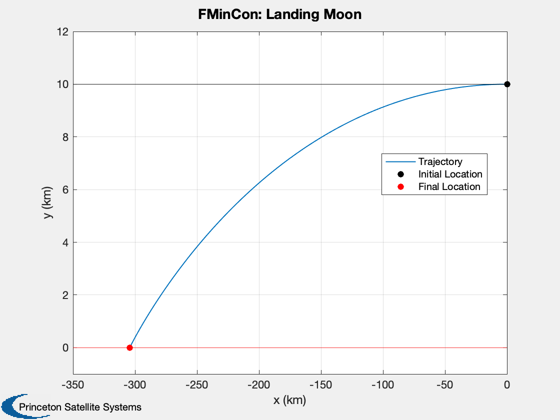
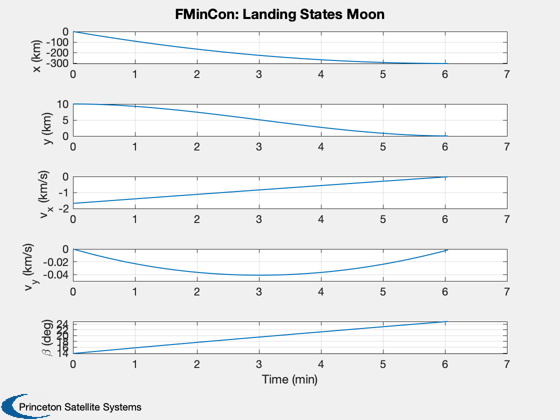
Print plots to a file

if( printFigures )
  PrintFig(0,2,3,'fmincon1');
  PrintFig(0,2,4,'fmincon2');
end


%--------------------------------------

Published with MATLAB® R2020a