Lunar Mission Demo
Simulate a mission from Earth orbit to lunar orbit. The spacecraft has 3 orthogonal reaction wheels and a single delta-v thruster. The mission plan does not perform the lunar insertion burn.
It uses the default values from RHSLunarMission for a 6U CubeSat. The dimensions are 30 x 20 x 10 cm.
Contents
%-------------------------------------------------------------------------- % Copyright (c) 2016 Princeton Satellite Systems, Inc. % All rights reserved. %-------------------------------------------------------------------------- % Since 2016.1 % 2020.1 Fixed the lunar insertion burn and the lunar orbit plotting %--------------------------------------------------------------------------
Constants
rMoon = 1738; dayToSec = 86400;
User inputs
dateEncounter = [2016 5 10 1 30 0]; % "Encounter" is passing into lunar sphere of influence dT = 2; % integration time step seconds el0 = [7000 0 0 0 0]; rLunarOrbit = 3000; % km incLunarOrbit = 1; surfaceMagnificationFactor = 10; % For lunar terrain display timeAdded = 36000; % sec added simulation time after intercept useSphericalHarmonics = 0;
Control setup
% Find transfer orbit to the moon jDEncounter = Date2JD( dateEncounter ); if( HasOptimizationToolbox ) [x0,el,~,jD0,jDP] = LunarTargeting( jDEncounter, el0, rLunarOrbit, incLunarOrbit, [], true ); else disp('LunarMission: Optimization toolbox not installed; using hard-coded values.') x0 = [-2.8408 6.3976 0 -0.0034 0.0099 0.0018]'*1e3; el = [-5.2588 0.0010 0.0001 0.0041 0.0016 0.0088]*1e3; jD0 = 2.457514449298204e+06; end tEnd = (jDP-jD0)*dayToSec + timeAdded; % Get the default data structure dC = LunarMissionControl; dC.dT = dT; dC = LunarMissionControl('initialize',jD0,dC); dRHS = RHSLunarMission; if( useSphericalHarmonics ) dRHS.sphHarmMoon = LoadSGM150( 'SGM150.geo' ); %#ok<*UNRCH> dRHS.sphHarmMoon.nN = 3; dRHS.sphHarmMoon.nM = 3; end % Set up the control data structure dC.mass = struct('mass',dRHS.mass,'inertia',dRHS.inertia,'cM',dRHS.surfData.cM); dC.rWA = dRHS.rWA; % This command list is for an lunar orbit insertion cList = { jDP-1e3/dayToSec,... 'lunar orbit insertion prepare',... struct('thrust',20,'massInitial',6, 'uE', 290*9.806,'body_vector',[1;0;0],'hLunarOrbit',200);... +2,... 'align for lunar insertion',... [];... +1e3,... 'start main engine',... struct('iD',1,'thrust',20)}; % Initial state setup qECIToBody = [1;0;0;0]; omega = [0;0;0]; % rad/s omegaRWA = [0;0;0]; % rad/s accelBias = [0;0;0]; % km/s^2 gyroBias = [0;0;0]; % rad/s massFuel = 3; % kg
Your initial point x0 is not between bounds lb and ub; FMINCON
shifted x0 to strictly satisfy the bounds.
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 5 1.055884e+01 4.365e+04 3.794e-03
1 12 1.056376e+01 4.004e+04 4.917e-03 4.157e-01
2 18 1.057372e+01 3.388e+04 1.746e-02 5.230e-01
3 23 1.058152e+01 2.375e+04 2.752e-02 5.975e-01
4 28 1.057247e+01 1.086e+03 4.815e-02 4.485e-01
5 34 1.057308e+01 8.566e+02 4.113e-02 7.109e-02
6 39 1.057413e+01 4.417e+02 5.429e-02 3.161e-01
7 44 1.057504e+01 1.233e+02 5.532e-02 2.619e-01
8 50 1.057980e+01 9.027e+01 6.054e-02 5.583e-01
9 57 1.058453e+01 6.990e+01 6.460e-02 2.839e-01
10 62 1.058210e+01 2.599e+01 2.468e-02 1.284e-01
11 68 1.057692e+01 7.241e+00 9.757e-03 4.175e-01
12 81 1.057558e+01 1.662e+00 3.650e-03 1.657e-01
13 94 1.057461e+01 1.502e+00 2.497e-03 1.579e-01
14 107 1.057423e+01 2.608e-01 2.066e-03 7.406e-02
15 120 1.057392e+01 2.451e-01 1.753e-03 7.221e-02
16 131 1.057366e+01 2.351e-01 1.471e-03 7.035e-02
17 142 1.057345e+01 2.232e-01 1.217e-03 6.854e-02
18 153 1.057327e+01 2.096e-01 9.918e-04 6.696e-02
19 164 1.057314e+01 1.947e-01 7.936e-04 6.594e-02
20 175 1.057303e+01 1.785e-01 6.224e-04 6.599e-02
21 186 1.057295e+01 1.611e-01 4.784e-04 6.781e-02
22 197 1.057289e+01 1.423e-01 3.614e-04 7.195e-02
23 208 1.057285e+01 1.222e-01 2.711e-04 7.839e-02
24 223 1.057282e+01 3.347e-02 2.056e-04 4.077e-02
25 236 1.057281e+01 3.136e-02 1.487e-04 4.251e-02
26 247 1.057279e+01 2.940e-02 9.999e-05 4.487e-02
Optimization completed: The relative first-order optimality measure, 9.999374e-05,
is less than options.OptimalityTolerance = 1.000000e-04, and the relative maximum constraint
violation, 6.735951e-07, is less than options.ConstraintTolerance = 1.000000e-04.
Hyperbolic Lunar Elements
Radius of perilune 3000.03 km
Semi major axis -5313.26 km
Inclination 57.30 deg
Longitude 6.40 deg
Perigee 235.11 deg
Eccentricity 1.56
Mean anomaly 496.50 deg
Start JD 2457514.4732 day
Transfer Time 4.0893 days
Initialize the simulation model
% Initialize JPL Ephemerides to include the Sun, Earth and Moon PlanetPosJPL( 'initialize', [0 3 10] ); nSim = ceil(tEnd/dT); dRHS.jD0 = jD0; x = [x0;qECIToBody;omega;massFuel;dRHS.power.batteryCapacity;... accelBias;gyroBias;omegaRWA]; % This initializes the state and auxiliary output names RHSLunarMission( x );
Run the simulation
t = 0; xP = zeros(length(x),nSim); [~, p] = RHSLunarMission( x, t, dRHS ); pP = zeros(length(p.auxNames),nSim); % Globals for the time tracking GUI global simulationAction simulationAction = ' '; for k = 1:nSim % Plot storage [~, p] = RHSLunarMission( x, t, dRHS ); q = x(7:10); xP(:,k) = x; pP(:,k) = p.aux; % The controller jD = jD0 + t/dayToSec; dC.rMoon = pP(21:23,k); dC.vMoon = pP(24:26,k); [dC, dRHS] = LunarMissionControl( 'update', jD, dC, dRHS, x, cList ); % Propagate x = RK4(@RHSLunarMission,x,dT,t,dRHS); t = t + dT; switch simulationAction case 'pause' pause simulationAction = ' '; case 'stop' LunarMissionControl( 'terminate' ); return; case 'plot' break; end end LunarMissionControl( 'terminate' );
jD 2457519.03193 lunar orbit insertion prepare jD 2457519.03195 align for lunar insertion jD 2457519.04352 start main engine
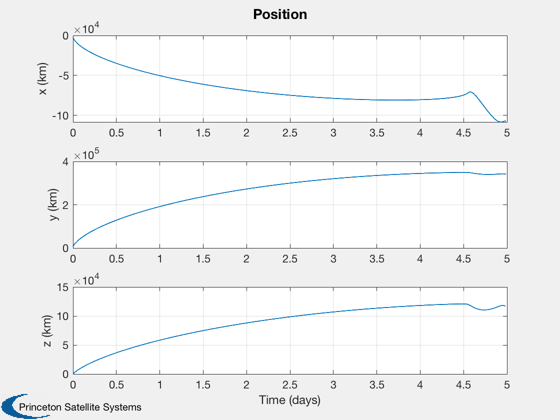
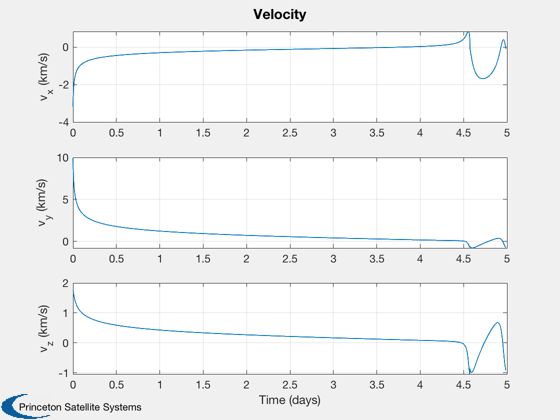
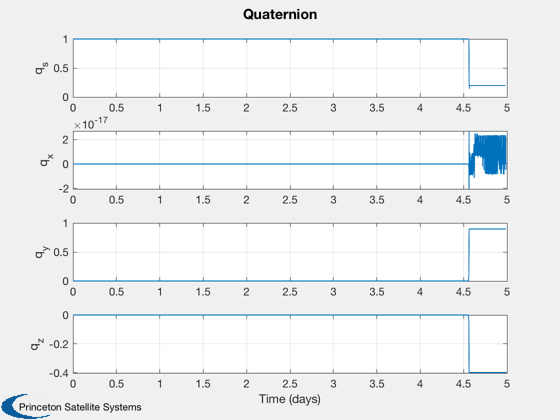
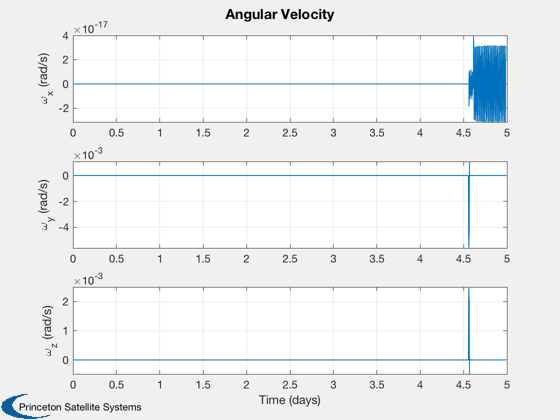
Plot the results
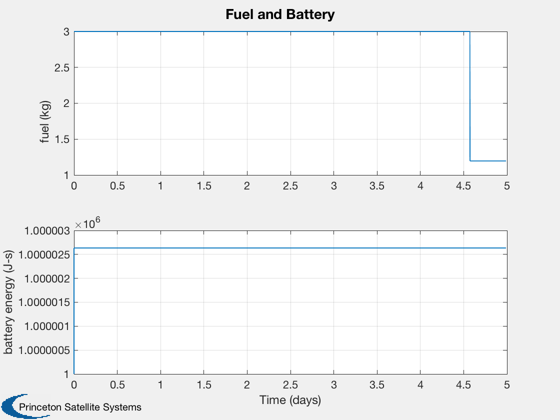
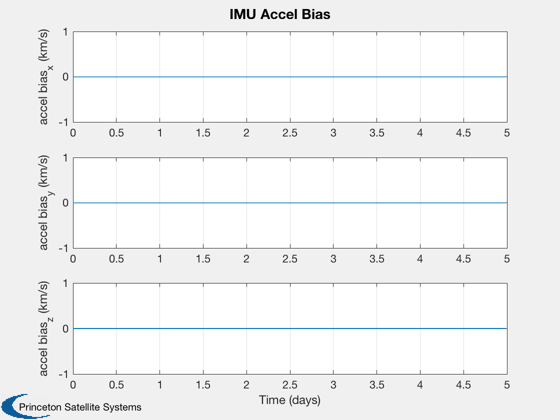
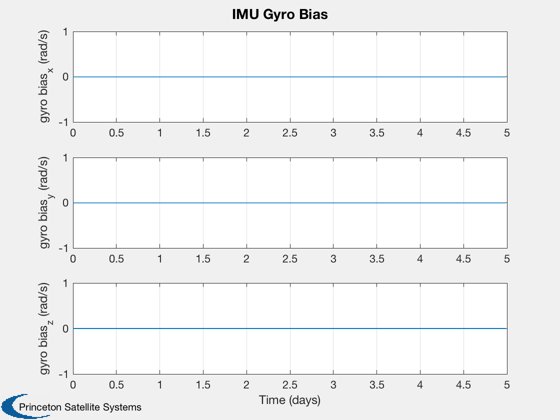
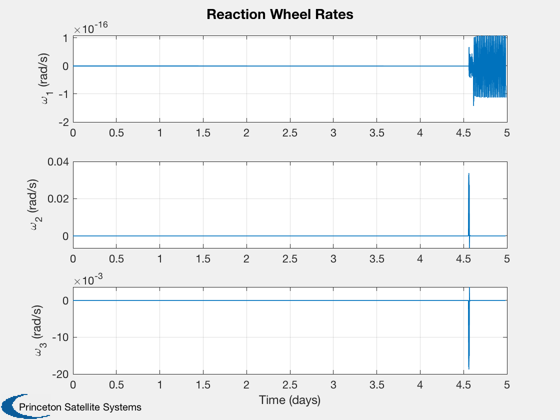
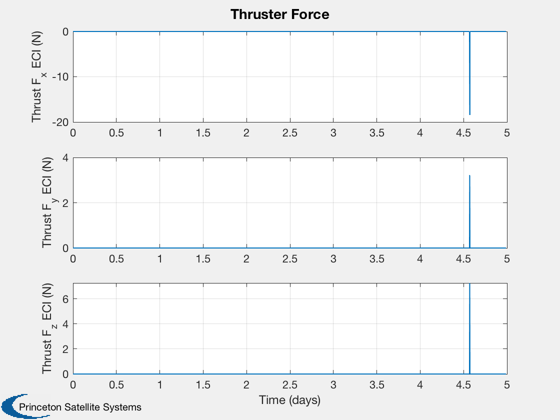
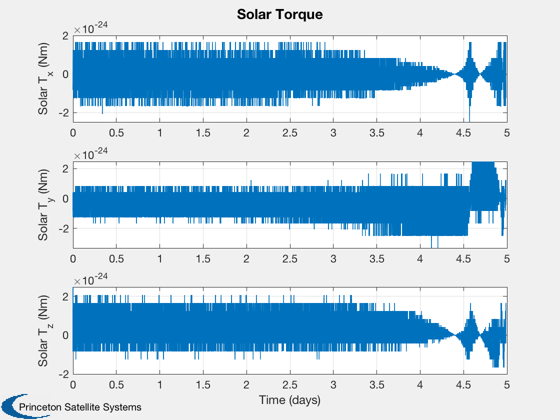
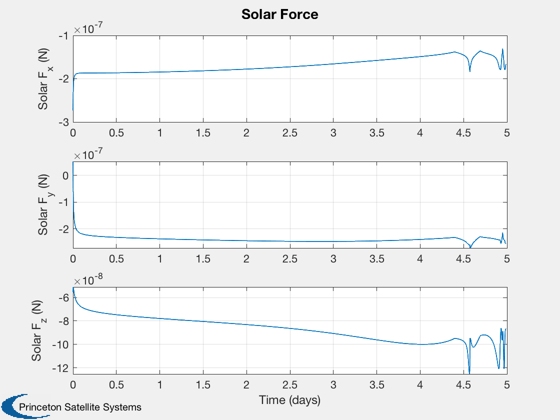
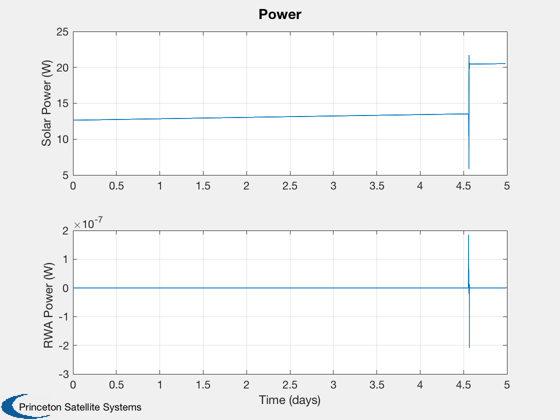
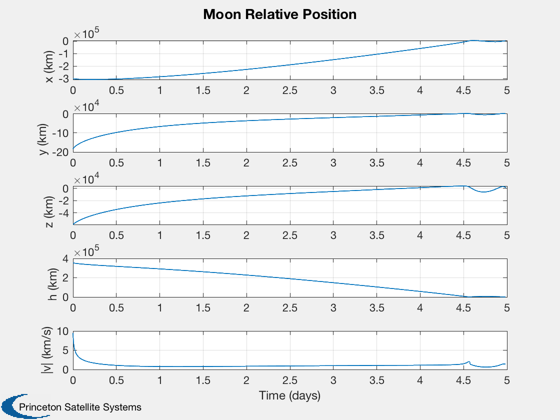
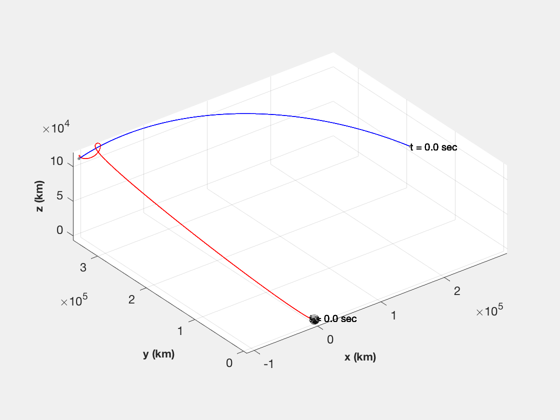
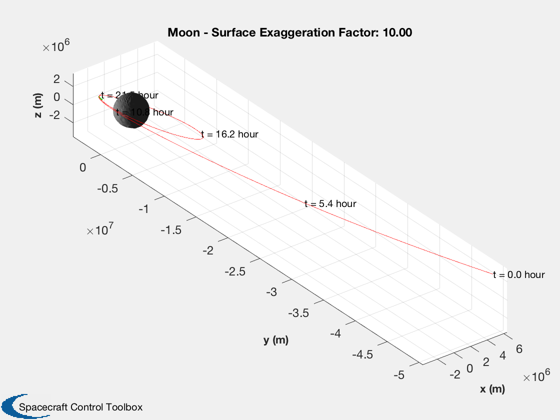
if k<nSim xP = xP(:,1:k); pP = pP(:,1:k); nSim = k; end tS = (0:nSim-1)*dT; jD = jD0 + t/dayToSec; % in days [t,tL] = TimeLabl(tS); % Plot the states k = 1:3; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Position'); k = 4:6; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Velocity'); k = 7:10; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Quaternion'); k = 11:13; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Angular Velocity'); k = 14:15; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Fuel and Battery'); k = 16:18; Plot2D(t,xP(k,:),tL,p.stateNames(k),'IMU Accel Bias'); k = 19:21; Plot2D(t,xP(k,:),tL,p.stateNames(k),'IMU Gyro Bias'); k = 22:24; Plot2D(t,xP(k,:),tL,p.stateNames(k),'Reaction Wheel Rates'); % Plot the auxiliary outputs k = 4:6; Plot2D(t,pP(k,:),tL,p.auxNames(k),'Thruster Force'); k = k+3; Plot2D(t,pP(k,:),tL,p.auxNames(k),'Solar Torque'); k = 10:12; Plot2D(t,pP(k,:),tL,p.auxNames(k),'Solar Force'); k = 13:14; Plot2D(t,pP(k,:),tL,p.auxNames(k),'Power'); k = 21:23; dR = xP(1:3,:) - pP(k,:); dV = Mag(xP(4:6,:) - pP(24:26,:)); h = Mag(dR) - rMoon; yL = {'x (km)', 'y (km)', 'z (km)', 'h (km)' '|v| (km/s)'}; Plot2D(t,[dR;h;dV],tL,yL,'Moon Relative Position'); % Plot the trajectory for the Earth/Moon transfer EarthMoon( xP(1:3,:), jD, [1, 1], pP(21:23,:) ); % Display from encounter time jD = jD0 + tS/dayToSec; kB = find(jD>jDEncounter); k = kB(1):nSim; dR = dR(:,k); jD = jD(1,k); uSun = SunV1(jD(1)); PlotLunarOrbit( dR, jD, uSun, pP(4:6,k), surfaceMagnificationFactor ); Figui; %--------------------------------------
ans = 126