Lunar polar mission planning

Compute lunar transfer delta-Vs. The steps are:

Set the elements and date so that transfer orbit and lunar orbit match.
Compute the insertion delta-v
Circularize the lunar orbit
Do a Hohmann descent to the powered landing altitude

Constants and parameters
ATK Star 26B TE-M-442-1
Transfer orbit
Compute the delta-vs
Insertion delta-V

%--------------------------------------------------------------------------
%   Copyright (c) 2015 Princeton Satellite Systems
%   All Rights Reserved.
%--------------------------------------------------------------------------
%   Since 2016.1
%--------------------------------------------------------------------------

Constants and parameters

The lander spacecraft is small, only 30 kg. We will be working in Earth-centered ecliptic coordinates for the transfer. The moon has a constant inclination with respect to the ecliptic plane.

rMoon         = Constant('equatorial radius moon');
muMoon        = Constant('mu moon');
gEarth        = Constant('accel grav mks');
muEarth       = Constant('mu earth');
kMToM         = 1000;

ATK Star 26B TE-M-442-1

iSpSolid      = 271.7;
fSSolid       = 0.09;
insEngine     = 'ATK Star 26B TE-M-442-1';

% hDescent is the altitude from which you begin the descent leg. Allow for
% the highest point on dark side, which is 6.5 km higher than Mons Huygens
% (altitude 4.7 km), and allow a margin of 0.3 km
hDescent     	= 6.5 + 4.7 + 0.3;

% Lunar orbit altitude
hLunarOrbit   = 200;
% Initial LEO altitude
rEarthParking	= 7000;
% Adjust this date until the orbits match
jD0               = Date2JD( [2016 5 11 1 30 0] );

% Work in the ecliptic frame
PlanetPosJPL( 'initialize', 10  );
[rJPL, mu, vJPL]	= PlanetPosJPL( 'update', jD0, 1  );
elM               = RV2El(rJPL,vJPL);

[mECIToS, uMoon]  = MoonRot(jD0);
uMoon             = Unit(uMoon);
iPolar            = asin(uMoon(3));

% Dry mass of the lander
massDry      	= 30;

% Specific impulse of the ECAPS LMP-103 engine
iSp          	= 285;

Transfer orbit

Generate a transfer orbit so that apogee is behind the moon. We need to match longitude, argument of perigee and inclination.

rLunarOrbit   = hLunarOrbit + rMoon;
rA            = elM(1)*(1+elM(5)) + rMoon + rLunarOrbit;
rP            = rEarthParking;
[aT,eT]       = RPRA2AE( rP, rA );
t             = linspace(0,Period(aT)/2,1000);
[rM, vM]      = RVOrbGen(elM,t); % Lunar orbit
[r, v]        = RVOrbGen([aT iPolar, 0 0 eT 0],t);
vTP           = VOrbit(rP,aT);

% Transform into ECI for simulation purposes
%-------------------------------------------
cEclToECI     = CEcl2Eq( jD0 );
dVIns         = vTP - sqrt(muEarth/rEarthParking);

% Plot the trajectory for the Earth/Moon transfer
%------------------------------------------------
jD = jD0 + t/86400; % in days
EarthMoon( r, jD, [1, 1], rM );

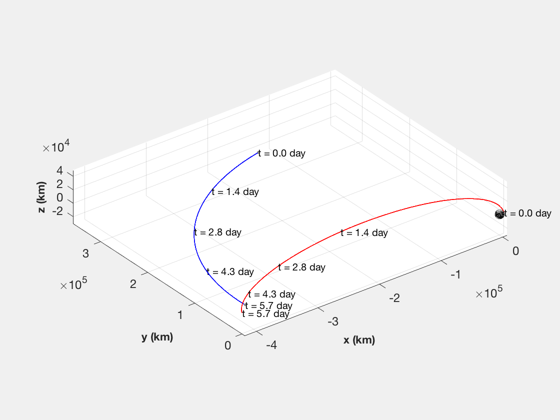
Compute the delta-vs

% Insertion from LEO
%-------------------
rP       = rMoon+hLunarOrbit;
rA       = Mag(r(:,end)-rM(:,end));
aM       = RARP2A( rP, rA );
vA       = VOrbit( rA, aM, muMoon );
vInf     = Mag(vM(:,end) - v(:,end));
vM       = sqrt(vInf^2 + muMoon/rA);
dV       = [];
dV(1)    = abs(vM-vA);

% Circularization of the lunar orbit
%-----------------------------------
vE       = VOrbit( rA, aM, muMoon );
vC       = sqrt(muMoon/rA);
dV(2)    = abs(vC - vE);

% Hohmann from lunar orbit altitude to hDescent
%----------------------------------------------
dV(3)    = DVHoh( rLunarOrbit, rMoon+hDescent, vC, muMoon  );

% Compute the mass ratio
%-----------------------
mR          = exp(sum(dV)*kMToM/(gEarth*iSp));
massFuel    = massDry*(mR-1);

Insertion delta-V

uE          = iSpSolid*gEarth;

[mF, mT]    = RocketMass( iSpSolid, massFuel+massDry, fSSolid, dVIns );
iIns        = iSpSolid*gEarth*mF/4.448;


clear s

k = 1;
s{k,1} = 'Julian Date';                   s{k,2} = sprintf('%9.2f days',jD0);       k = k + 1;
s{k,1} = 'Transfer Orbit   $\Delta V$';   s{k,2} = sprintf('%4.2f km/s',dVIns);     k = k + 1;
s{k,1} = 'Transfer stage mass';           s{k,2} = sprintf('%4.2f kg',mT);          k = k + 1;
s{k,1} = 'Insertion Impulse';             s{k,2} = sprintf('%4.2f lbf-s',iIns);     k = k + 1;
s{k,1} = 'Insertion Engine';              s{k,2} = insEngine;                       k = k + 1;
s{k,1} = 'Transfer Orbit   $\Delta V$';   s{k,2} = sprintf('%4.2f km/s',dVIns);     k = k + 1;
s{k,1} = 'V$_infty$';                     s{k,2} = sprintf('%4.2f km/s',vInf);      k = k + 1;
s{k,1} = 'Perigee altitude lunar orbit';	s{k,2} = sprintf('%4.2f km',rP-rMoon);    k = k + 1;
s{k,1} = 'Circular orbit altitude';       s{k,2} = sprintf('%4.2f km',hLunarOrbit); k = k + 1;
s{k,1} = 'Descent orbit altitude';        s{k,2} = sprintf('%4.2f km',hDescent);    k = k + 1;
s{k,1} = 'Insertion $\Delta V$';          s{k,2} = sprintf('%4.3f km/s',dV(1));     k = k + 1;
s{k,1} = 'Circularization  $\Delta V$';   s{k,2} = sprintf('%4.3f km/s',dV(2));     k = k + 1;
s{k,1} = 'Orbit lowering  $\Delta V$';    s{k,2} = sprintf('%4.3f km/s',dV(3));     k = k + 1;
s{k,1} = 'Mission total  $\Delta V$';     s{k,2} = sprintf('%4.2f km/s',sum(dV));   k = k + 1;
s{k,1} = 'Mass dry';                      s{k,2} = sprintf('%4.2f kg',massDry);     k = k + 1;
s{k,1} = 'Mass fuel';                     s{k,2} = sprintf('%4.2f kg',massFuel);    k = k + 1;

thisPath = fileparts(mfilename('fullpath'));
DisplayLatexTable(s);

CreateLatexTable(s,fullfile(thisPath,'EarthMoonTransfer'))


%--------------------------------------
% PSS internal file version information
%--------------------------------------