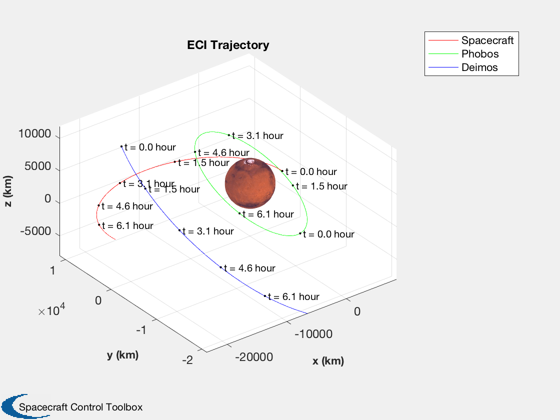
Spacecraft simulation around Mars with Phobos and Deimos
You can select orbital elements for the spaceraft The initial states for Phobos and Deimos are from the NASA Horizons system. http://ssd.jpl.nasa.gov/horizons.cgi Uses RK4 to propagate the orbits.
Contents
%-------------------------------------------------------------------------- % Copyright (c) 2016 Princeton Satellite Systems, Inc. % All Rights Reserved. %-------------------------------------------------------------------------- % Since 2017.1 %-------------------------------------------------------------------------- % Constants muMars = Constant('mu mars'); rMars = Constant('equatorial radius mars'); % User inputs hP = 2000; % Altitude at perigee [a,e] = RPRA2AE(rMars+hP, rMars+10*hP); i = 0; % Inclination lon = 0; % Longitude of the ascending node arg = 0; % Argument of perigee meanA = 0; % Mean anomaly tEnd = 7.6538*3600; % One Deimos orbit period is 30.312 hours Phobos is 7.6538 hours dT = 100;
Create the state vector [spacecraft;phobos;deimos]
jD0 = 2457504.5; xMars = [-1.556270572128525E+08 -1.588260151341932E+08 -6.864850347069533E+07... 1.892393454800366E+01 -1.265972881093017E+01 -6.317572782411839E+00]'; xDeimos = [-1.556471976805823E+08 -1.588240996199218E+08 -6.863662644229279E+07... 1.853761291642451E+01 -1.387018839272505E+01 -6.776942570158258E+00]'; xPhobos = [-1.556243982587785E+08 -1.588334963677697E+08 -6.865370813242640E+07... 2.070933433329652E+01 -1.167145060591693E+01 -6.857269178105281E+00]'; % Spacecraft state [r,v] = El2RV([a i lon arg e meanA],[],muMars); % Full state vector x = [r;v;xPhobos-xMars;xDeimos-xMars];
Simulation
n = ceil(tEnd/dT); % Total number of integration steps xP = zeros(length(x),n); dT = tEnd/n; for k = 1:n xP(:,k) = x; x = RK4(@RHSMarsOrbit,x,dT,0,muMars); end
Plotting
jD = jD0 + (0:n-1)*dT/86400;
PlotPlanetOrbit( xP, jD, {'Spacecraft' 'Phobos' 'Deimos'}, 'Mars', 1 );
%--------------------------------------