Pluto mission delta-Vs using DFD, Lambert solutions

Use Lambert to calculate the delta-V to Pluto over a range of transit times, from 2 to 10 years. Estimate the total mission mass using specific power to scale the spacecraft, plus allowing for a given tank fraction, thrust efficiency, and a payload of 1000 kg.

See also Constant, SaveStructure, Plot2D, Plot3D, Date2JD, RK4, Mag, LambertTOF, VEscape, RocketMass, FOrbCart, RV2El, PlanetPosition

Script parameters
Lambert analysis
Plot the mission

%--------------------------------------------------------------------------
%   Copyright (c) 2015 Princeton Satellite Systems, Inc.
%   All Rights Reserved.
%--------------------------------------------------------------------------
%   Since version 2016.1
%--------------------------------------------------------------------------

Script parameters

These are the parameters that define the mission analysis. For simplicity we must assume a fixed thrust and Isp throughout the mission. The engine mass will be calculated solely based on the specific power.

% Payload mass (kg)
mPLD      = 1000;
% Assume a specific power
kWPerKg   = 1.2;
% Total engine power
power     = 2e6; % W
% Tank structural fraction
tankF     = 0.02;
% Engine thrust
thrust    = 20;  % N
% Engine efficiency
eff       = 0.5;

% orbital altitude at Pluto (km)
h         = 600;
% Epoch
jD0        = Date2JD([2028 7 2 0 0 0]);

% Fusion fuel computations
He3_STP = 0.1339;
rho3He = 59;                % density of liquid 3He, kg/m3
amu3He = 1.6605e-27*3.016;  % mass of 3He atom, kg
ePerReaction = 18.3;        % MeV, energy per D-3He reaction
eJPerReaction = ePerReaction*1e6*1.602e-19; % J per reaction

Lambert analysis

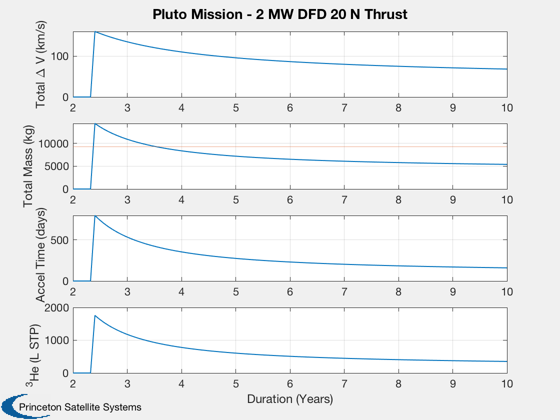
Perform an analysis of the transfer to Pluto for an array of mission durations.

% Constants
muSun     = Constant('mu sun');
muPluto   = Constant('mu pluto');
rPluto    = Constant('equatorial radius pluto');
aU        = Constant('au');

% Mass of the engine, using specific power
massDFD   = power/kWPerKg/1000;

% Exhaust velocity - will be fixed
uE        = 2*power*eff/thrust;

PlanetPosition( 'initialize', [3 9] );
[r0, ~, v]  = PlanetPosition( 'update', jD0 );
dVOrbit     = VEscape(rPluto+h,muPluto) - sqrt(muPluto/(rPluto+h));

years       = linspace(2,10);
n           = length(years);
dV          = zeros(1,n);
mF          = zeros(1,n);
mT          = zeros(1,n);
tAccel      = zeros(1,n);
hE3         = zeros(1,n);
for k = 1:n
  duration      = years(k)*365.25;
  [rI, ~, vI]   = PlanetPosition( 'update', jD0+duration );
  vT            = LambertTOF( r0(:,1), rI(:,2), duration*86400, 1, muSun );

  dV(k)         = Mag(vT(:,1) - v(:,1)) + Mag(vT(:,2) - vI(:,2));

  dVTotal       = dV(k) + dVOrbit;
  [mF(k),mT(k)] = RocketMass( uE/9.806, mPLD+massDFD, tankF, dVTotal );
  accel         = thrust/(mT(k) - 0.5*mF(k));
  tAccel(k)     = dV(k)*1000/accel/86400;

  % if available, see He3MassFromPower
  if exist('He3MassFromPower','file')
    [~,~,vol]   = He3MassFromPower( power*tAccel(k)*86400 );
    hE3(k)      = vol(1);
  else
    energy      = power*tAccel(k)*86400;
    mass3He     = amu3He*energy/eJPerReaction;
    hE3(k)      = mass3He*1e3/He3_STP;
  end

  if tAccel(k)>duration
    tAccel(k) = 0;
    dV(k) = 0;
    mF(k) = 0;
    mT(k) = 0;
    hE3(k) = 0;
  end
end

yL = {'Total \Delta V (km/s)' 'Total Mass (kg)' 'Accel Time (days)' '^3He (L STP)'};
titleStr = sprintf('Pluto Mission - %d MW DFD %d N Thrust',round(power/1e6),round(thrust));
Plot2D(years,[dV;mT;tAccel;hE3],'Duration (Years)', yL,titleStr)
subplot(4,1,2)
hold on
yy = axis;
plot(yy(1:2),9306*[1 1])

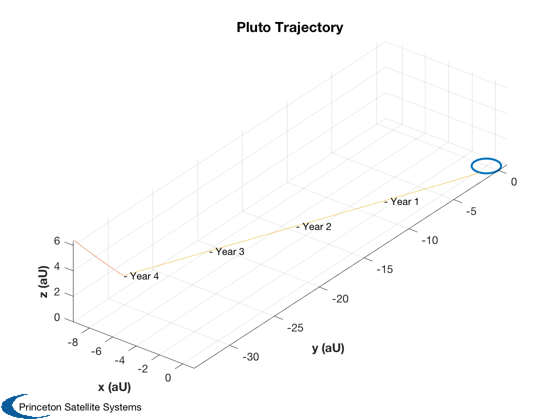
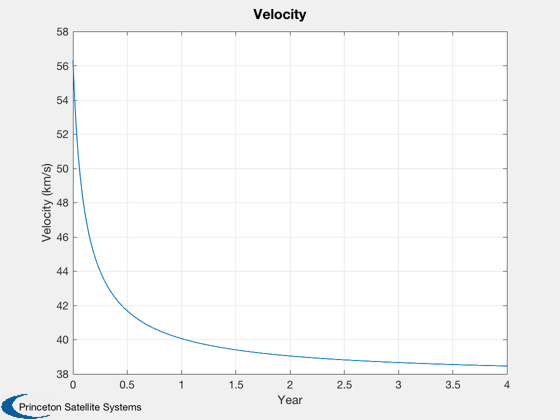
Plot the mission

yearsMission  = 4; % selected from prior plot
duration      = yearsMission*365.25;
[rI, ~, vI]   = PlanetPosition( 'update', jD0+duration );
[vT, a]       = LambertTOF( r0(:,1), rI(:,2), duration*86400, 1, muSun );
dV            = Mag(vT(:,1) - v(:,1)) + Mag(vT(:,2) - vI(:,2));
dVTotal       = dV + dVOrbit;

[massFuelPluto, massTotalPluto] = RocketMass( uE/9.806, mPLD+massDFD, tankF, dVTotal );

accel         = thrust/(massTotalPluto - 0.5*massFuelPluto);

% Calculate the 3He mass for the mission. See also He3MassFromPower in the
% FusionPropulsion module, if available.
tAccel        = dV*1000/accel/86400;
energy3He     = 18.3*1.6e-19*1e6;   % J per D-3He reaction
energyTotal   = power*tAccel*86400; % accel time only
mHe3          = 5.0082e-27; % kg
massHe3       = mHe3*energyTotal/energy3He;

% Perform a point-mass heliocentric simulation
n             = 1000;
rE            = zeros(3,n);
rP            = zeros(3,n);
vM            = zeros(1,n);
day           = jD0 + linspace(0,duration,n);
x             = [r0(:,1);vT(:,1)]; % Note the 25% increase in velocity
rT            = zeros(3,n);
el            = RV2El(x(1:3),x(4:6),muSun);
dT            = (day(2)-day(1))*86400; % sec

for k = 1:n
  r       = PlanetPosition('update',day(k));
  rE(:,k) = r(:,1);
  rP(:,k) = r(:,2);
  rT(:,k) = x(1:3);
  vM(1,k) = Mag(x(4:6));
  x       = RK4(@FOrbCart,x,dT,0,[0;0;0],muSun);
end

% Plot the trajectory with the planet orbits
rE = rE/aU;
rP = rP/aU;
rT = rT/aU;
Plot3D( rE, 'x (aU)', 'y (aU)', 'z (aU)', 'Pluto Trajectory' )
hold on
plot3(rP(1,:),rP(2,:),rP(3,:));
plot3(rT(1,:),rT(2,:),rT(3,:));
% Add year labels
year = (day - jD0)/365.25;
j    = ceil(linspace(1,n,5));
for k = 2:5
  i = j(k);
  text(rT(1,i), rT(2,i), rT(3,i),sprintf('- Year %d',floor(year(i))));
end

% Plot the velocity magnitude
Plot2D(year,vM,'Year','Velocity (km/s)','Velocity')

% Store mission data
q           = struct;
q.massHe3   = massHe3;
q.massFuel  = massFuelPluto;
q.massDFD   = massDFD;
q.massPld   = mPLD;
q.power     = power;
q.specPower = kWPerKg;
thisP       = fileparts(mfilename('fullpath'));
SaveStructure(q,fullfile(thisP,'PlutoSpacecraftData'));


%--------------------------------------

Pluto mission delta-Vs using DFD, Lambert solutions

Contents

Script parameters

Lambert analysis

Plot the mission