Contents

Momentum unloading with magnetic torque

Perform a long-term simulation of just the momentum unloading using magnetic torque. Performs Euler integration of the momentum vector in the ECI frame. This shows how the 3 axis torque is met over the course of the orbit depsite the mismatch at each time step.

See also MomentumUnloading, PlotOrbit, Period, RVOrbGen, BDipole, Figui, TimeHistory, Date2JD, Skew

%--------------------------------------------------------------------------
%   Copyright (c) 2025 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2025.1
%--------------------------------------------------------------------------

% Momentum control gain
gain    = 0.001;

% Initial momentum (Nms)
h   = [1;1;1];

% Spacecraft semi-major axis
sMA     = 6728; % km

jD0     = Date2JD([2029 6 1]);
n       = 10000; % Number of steps

% Orbit
el      = [sMA 28.573469*pi/180 pi 0 0 0];
p       = Period(sMA);
t       = linspace(0,100*p,n);
[r,v,t] = RVOrbGen(el,t);
jD      = jD0 + t/86400;
b       = BDipole(r,jD);

Run the simulation

xP  = zeros(15,n);
for k = 1:n
  [tM, m, ~, tD] = MomentumUnloading( b(:,k), gain, h );
  xP(:,k) = [b(:,k);m;h;tD;tM];
  h       = h + dT*tM; % Euler integration
end

Plotting

yL     = {'B_x (T) ' 'B_y (T)' 'B_z (T)' ...
          'M_x (ATM) ' 'M_y (ATM)' 'M_z (ATM)' ...
          'H_x (Nms) ' 'H_y (Nms)' 'H_z (Nms)' ...
          'T_{d_x} (Nm)' 'T_{d_y} (Nm)' 'T_{d_z} (Nm)'...
          'T_{m_x} (Nm)' 'T_{m_y} (Nm)' 'T_{m_z} (Nm)'};

PlotOrbit(r,t,jD0);

k = 1:6;
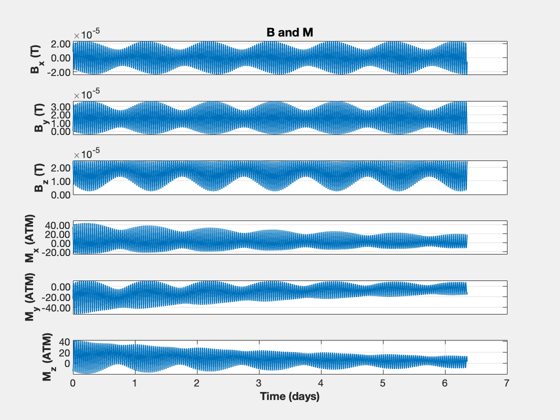
TimeHistory(t,xP(k,:),yL(k),'B and M');

k = 4:9;
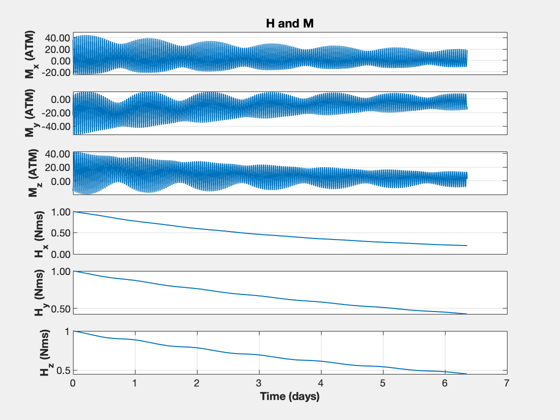
TimeHistory(t,xP(k,:),yL(k),'H and M');

k = 10:15;
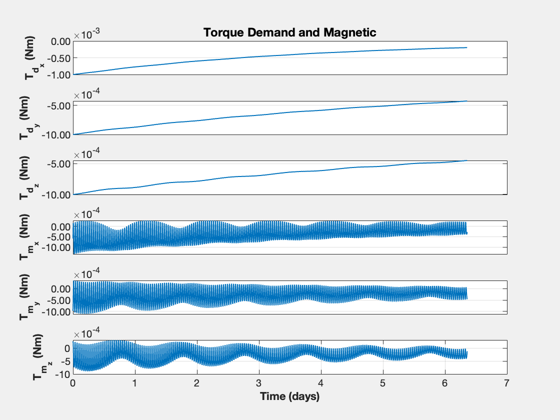
TimeHistory(t,xP(k,:),yL(k),'Torque Demand and Magnetic');

Figui


%--------------------------------------

% $Id: f71ed867fad289172a702d47fd815a64a6ea6bb9 $

Published with MATLAB® R2024a